Курсовая работа: Вариации при исчислении

Пусть функция подчиняется всем оговоренным выше условиям, тогда уравнение (1.50) принимает вид

. (1.51)

1.12 Функционал от функций, имеющих производные высших порядков

Рассмотрим функционал вида

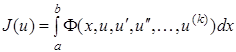. (1.52)

Будем считать, что функция определена в области

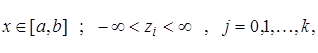
и в этой области k раз непрерывно дифференцируема.

Функционал (1.52) зададим на функциях , удовлетворяющих краевым условиям

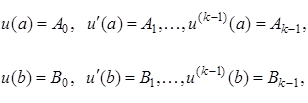(1.53)

где Ai, Bi– заданные постоянные. Возьмем функцию в виде , чтобы удовлетворялись требования 1,2,3 и составим функционал

(1.54)

Пусть функция такова, что имеет обобщенную производную j-го порядка, тогда

и, следовательно,

(1.55)

Откуда получим уравнение Эйлера

(1.56)

с краевыми условиями (1.53).

Сказанное выше переносится на случай функции многих независимых переменных. Для функционала

(1.57)

при краевых условиях

(1.58)

где – нормаль к Г.

Уравнение Остроградского будет иметь вид

(1.59)

Это уравнение должно решаться при краевых условиях (1.58)

Пример.

Выражение полной энергии деформации жесткой пластинки (плиты) при малых перемещениях, находящейся под действием поперечной нагрузки , представляет собой функционал вида