Курсовая работа: Визначення характеристик вала з дисками
Для рішення вартої перед нами завдання зручніше за все скористатися рівняннями руху Лагранжа, тому, насамперед, знайдемо кінетичну й потенційну енергію нашої системи.
Кінетична енергія системи буде складатися з кінетичної енергії диска й кінетичної енергії вала. Кінетична енергія диска
Для знаходження кінетичної Енергії вала спочатку знайдемо кінетичну енергію елемента його dc. Якщо кут закручування в перетині з позначити
, то кінетична енергія елемента dc буде
тому що якщо 
— момент інерції одиниці довжини, то I0 'dc момент інерції елемента dc.
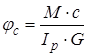Знайдемо залежність між кутом закручування в перетині з-с-і в перетині 
і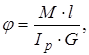 
Звідки
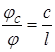
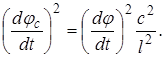
Підставляючи отримане значення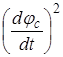 
у вираження кінетичної енергії елемента dc, одержимо:
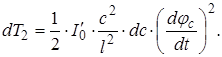
Повну кінетичну енергію вала знайдемо інтегруванням:
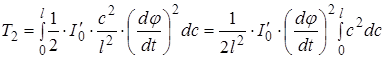
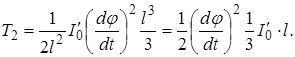
Або заміняючи на основі формул (b) і (с) на 
одержимо остаточно:
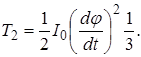
Повна кінетична енергія системи
коливання вад диск спектральний
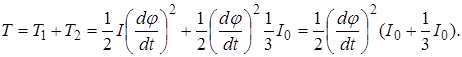
Потенційна енергія системи
де M - крутний момент, прикладений до вала. Для крутний моменту маємо вираження:
(1.1а)
Підставляючи це значення у вираження для потенційної енергії, одержимо:
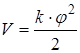(2.1)
Тепер можемо скласти диференціальне рівняння коливального руху нашого вала, що зручніше за все зробити у формі Лагранжа. У нашім випадку за узагальнену координату необхідно прийняти кут закручування 
, тоді рівняння Лагранжа прийме вид: