Курсовая работа: Визначення характеристик вала з дисками

у цьому рівнянні

Знаходимо значення часток похідних, що входять у це рівняння:

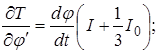
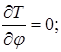
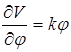
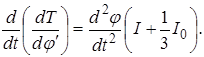
Підставимо отримані значення в рівняння Лагранжа

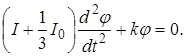
Звільняючись від коефіцієнта при диференціалі й думаючи

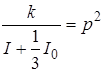
одержимо

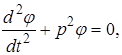
відоме нам рівняння (1.3), рішення якого

.

Частота цього коливального руху

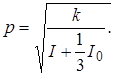
І період

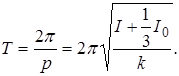(2.2)

Отже, для обліку власної маси вала, що має коливання, необхідно до моменту інерції диска, що сидить на валу, додати одну третину моменту інерції вала.

Розглянемо випадок вала, що лежить у двох підшипниках (вплив яких на коливання ми, у виді незначності, не враховуємо), що несе на кінцях два диски (маховика, шківа й т.д.) (малюнок 2).

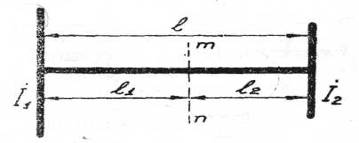
Мал. 2 Вал із двома дисками

Вал буде випробовувати крутильні коливання тільки за умови обертання дисків у різні сторони, що може бути досягнуто додатком до дисків двох рівних і прямо протилежних моментів. Після видалення моментів у системі, що складається з вала й двох; дисків, виникнуть крутильні коливання. У кожний момент часу кутові швидкості дисків будуть спрямовані протилежно один одному. Лівий диск і деяка частина вала, що примикає до нього, буде обертатися, допустимо, за годинниковою стрілкою, а правий диск і його частина вала проти годинникової стрілки. У такому випадку на валу обов'язково повинне бути перетин, у якому немає ніякого обертання. Вал можна розглядати як жорстко забитий у перетині, причому, у нашім прикладі, ліва частина обертається по вартовий і права проти годинникової стрілки.

Перетин, що залишається під час коливання системи нерухливим, називається вузлом коливання.

Періоди коливань однакові для обох частин того самого вала можуть бути знайдені з формули (1.6),

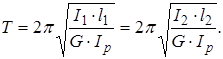(2.3)

Завдання, таким чином, зводиться до визначення розташування вузла коливань по довжині вала, тобто довжин l₁ і l₂ . Рівняння (2.3) показує, що вузол коливання ділить вал назад пропорційно моментам інерції дисків, тобто

або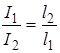

Друге рівняння для визначення положення вузла коливань буде

З рівнянь одержимо