Курсовая работа: Визначення характеристик вала з дисками

і період коливання прийме вид

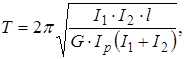(2.4)

частота коливань буде:

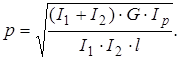(2.5)

Для вивчення випадків коливання валів з більшим числом дисків, чим два, зручніше на відміну від вищенаведених випадків вала з однієї й двома масами знайти рівняння руху вала з довільною кількістю мас і потім застосовувати його для будь-якої частки випадку.

1.2 Рішення прямого завдання для вала з n-дисками

Розглянемо вал, що несе дисків. Нехай кути закручування вала в місцях насадки диска будуть відповідно Твердості I, II,..., n-1 ділянок вала, тобто на основі позначення (1.1) моменти, які можуть викликати кут закручування даної ділянки рівний одному радіану, позначимо: k₁ , k_2,…, k_п-1. Моменти інерції дисків як і раніше позначимо I₁ ,I₂ ,..,I_n . Для одержання рівняння коливального руху розглянутої нами системи застосуємо рівняння Лагранжа, при користуванні якими необхідно знати вираження для кінетичної й потенційної енергії системи. Кінетична енергія диска, що має момент інерції I і кут закручування , виражається формулою

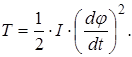
Кінетична енергія нашої системи складається із суми кінетичної енергії всіх дисків (кінетичну енергію вала ми отут не враховуємо, уважаючи момент інерції диска більшим у порівнянні з моментом інерції вала).

Кінетична енергія всієї системи

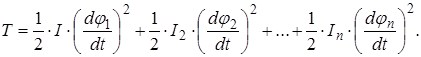(2.6)

Для знаходження потенційної енергії системи, що є в цьому випадку енергією крутіння, необхідно користуватися формулою

,

де М - крутний момент, що діє на даній ділянці, а - кут закручування тієї ж ділянки. Знайдемо крутний момент і кут закручування для першої ділянки нашої системи.

Якщо в місці насадки першого диска кут закручування , а в місці насадки другого диска — ₂ , то кут закручування на ділянці вала між дисками буде:

(2.7)

Для того щоб викликати кут закручування першої ділянки вала завбільшки I радіан, необхідно прикласти крутний момент величини k₁ , якщо ж, як у нашім випадку кут закручування має ₁ -₂ радіан, то на валу діє крутний момент величини

У нашім випадку кути закручування для ділянок вала будуть:

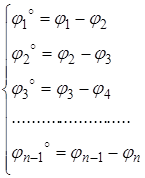(2.8)

і крутний моменти:

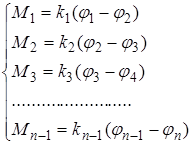(2.9)

Тепер можемо скласти вираження для потенційної енергії системи, підсумовуючи потенційну енергію ділянок.

(2.10)

(тому що те, підставляючи значення ₁ з (2.8) і M₁ з (2.9) і аналогічно для інших ділянок одержимо формулу (2.10)).

У цьому випадку система має п ступенів волі, чому відповідає п узагальнених координат. Узагальненими координатами є кути закручування вала в місцях насадки дисків. Рівняння Лагранжа, мабуть, прийде скласти по числу ступенів волі, тобто також п. Для користування рівнянням Лагранжа у вигляді

(2.11)

необхідно знайти частки похідні від кінетичної й потенційної енергії системи, по узагальнених координатах і частки похідні від кінетичної енергії по диференціалах узагальнених координат: