Курсовая работа: Власні значення і власні вектори матриці

0

1,5

1

0,5

1

2,5

2

1,5

0

–3,5

–1

3,5

1

–5

–2

3

0

7’ –24 –15 11 19 –9 ІІ –1,600

–0,067

–1

0,733 1,267 –0,600 9 –24 –1 0,167 –0,333 –0,667 –1,833 –2 10 –15 1,2 0,133 –0,467 –0,533 0,333 0,2 11 11 0 1 0 0 1 0 12 19 0 0 1 0 1 1 10’ 6 5 34 24 69 ІІІ 0,167–1 –0,833 –5,667 –4,000 –11,500 13 6 –0,167 1 5,333 3,333 9,500 9,667 14 5 1 0 0 0 1 0 15 34 0 1 0 0 1 1 16 24 0 0 1 0 1 1 13’ 4 40 56 20 120

У рядках 1-4 таблиці 1 розміщуємо елементи даної матриці і контрольні суми 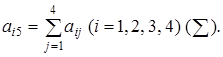. Відзначаємо елемент , що належить третьому стовпцю (відмічений стовпець). У рядку 1 записуємо елементи третього рядка матриці , що обчислюються за формулами (4) і (4'):

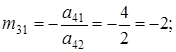
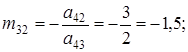
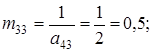
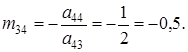
Сюди ж (рядок 1 таблиці 1) поміщаємо елемент

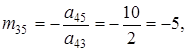
що одержується аналогічним прийомом з контрольного стовпця Σ. Число -5 повинно співпасти з сумою елементів рядка I, що не входять в контрольний стовпець (після заміни елементу на -1). Для зручності число -1 записуємо поряд з елементом , відокремлюючи від останнього межею.

У рядках 5-8 в графі М^-1 виписуємо третій рядок матриці М^-1 , яка в силу формули (7) співпадає з четвертим рядком початкової матриці А. У рядках 5-8 у відповідних стовпцях виписуємо елементи матриці

B = АМ₃ ,