Курсовая работа: Власні значення і власні вектори матриці
Отже
(8)
Оскільки, очевидно, множення зліва матриці 
на матрицю В не змінює перетвореного рядка останньої, то матриця C має вигляд
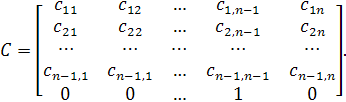(9)
Перемножуючи матриці (7) і B (5), матимемо:
(10)
І
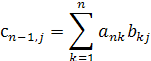
(10')
Таким чином, множення на матрицю В змінює лише (n - 1) -й рядок матриці В. Елементи цього рядка знаходяться за формулами (10) і (10'). Одержана матриця C подібна матриці А і має один зведений рядок. Цим закінчується перший етап процесу.
Далі, якщо 
, то над матрицею C можна повторити аналогічні операції, узявши за основу (n - 2) -й її рядок. В результаті одержимо матрицю
з двома зведеними рядками. Над останньою матрицею проробляємо ті ж операції. Продовжуючи цей процес, ми, нарешті, одержимо матрицю Фробеніуса
якщо, звичайно, всі n - 1 проміжних перетворень можливі. Весь процес може бути оформлений в зручну обчислювальну схему, складання якої покажемо на наступному прикладі.
Приклад. Привести до вигляду Фробеніуса матрицю
.
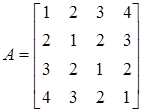Розв’язання.
Обчислення розташовуємо в таблицю 1.
|
Номер рядка |  | Рядки матриці | Σ | Σ’ | |||
| 1 | 2 | 3 | 4 | ||||
|
1 2 3 4 |
1 2 3 4 |
К-во Просмотров: 483
Бесплатно скачать Курсовая работа: Власні значення і власні вектори матриці
| |||||