Курсовая работа: Власні значення і власні вектори матриці

,

і, значить, всі натуральні степені однієї і тієї ж матриці переставні між собою.

Справедливе й більш загальне твердження: якщо матриці А і В переставні, то будь-які їх натуральні степені також переставні й для будь-якого натурального p маємо

Транспонування матриць.

Розглянемо довільну матрицю

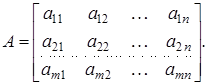
Матриця

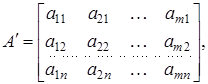
що отрималася з А заміною рядків стовпцями, називається транспонованою по відношенню до А.

Для довільних матриць А, В мають місце наступні правила транспонування:

,

де, α, β — довільні числа.

Якщо А — довільна квадратна матриця і

то А називається симетричною; якщо ж

то — кососиметричною. [4]

Поняття визначника. Розглянемо довільну квадратну матрицю будь-якого порядку n:

Визначник (або детермінант) визначається для довільної квадратної матриці А, і являє собою поліном від всіх її елементів. Позначається — або det(A), або — в розгорнутому вигляді

(матриця обмежується вертикальними лініями). Маючи на увазі порядок матриці А, про її визначник кажуть як про визначник порядку п.

Для п=1:

для п=2:

для п=3: