Курсовая работа: Власні значення і власні вектори матриці

[4]

Добутком матриці , що має відповідно розмірність m х n, на матрицю , що має відповідно розмірність n х p, називається матриця , що має відповідно розмірність m х p,та елементи , які визначаються за формулою

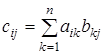
(1)

Для позначення добутку матриці А на матрицю В використовують запис . Операція складання добутку матриці А на матрицю В називається перемноженням цих матриць.

Зі сформульованого вище слідує, що матрицю А можна помножити не на будь-яку матрицю В: необхідно, щоб кількість стовпців матриці А дорівнювало кількості рядків матриці В.

Зокрема, два добутки можна визначити лише в тому випадку, коли кількість стовпців А співпадає з числом рядків В, а кількість рядків А співпадає з кількістю стовпців В. При цьому обидві матриці будуть квадратними, але порядки їх будуть різними. Для того щоб обидва добутки не тільки були визначеними, але й мали однаковий порядок, необхідно і достатньо, щоб обидві матриці А і В були квадратними матрицями одного й того ж порядку.

Формула (1) являє собою правило складання елементів матриці С, що являє собою добуток матриці А на матрицю В. Це правило можна сформулювати і словесно: елемент , що стоїть на перетині і-го рядка та j-го стовпця матриці , дорівнює сумі попарних добутків відповідних елементів і-го рядка матриці А та j-го стовпця матриці В.

В якості приклада застосування вказаного правила приведемо формулу перемноження квадратних матриць другого порядку

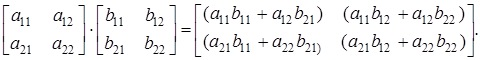
З формули (1) витікають наступні властивості добутку матриці А на матрицю В:

1.

2. або

Серед квадратних матриць виділимо клас так званих діагональних матриць, у кожної з яких елементи, що розташовані не на головній діагоналі, дорівнюють нулю. Кожна діагональна матриця має вид

,

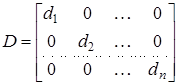де — які завгодно числа. Легко бачити, що якщо всі ці числа рівні між собою, тобто то для будь-якої квадратної матриці А порядку n справедлива рівність .

Серед усіх діагональних матриць, у яких діагональні елементи співпадають особливу роль відіграють дві матриці. Перша з них отримується при d = 1, називається одиничною матрицею n-го порядку і позначається Е. Друга матриця отримується при d = 0, називається нульовою матрицею n-го порядку і позначається О.

Таким чином,

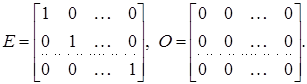
[2, стор. 14]

З правил дій над матрицями безпосередньо витікає, що сумма і добуток діагональних матриць буде знову діагональною матрицею:

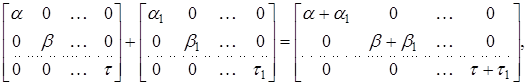
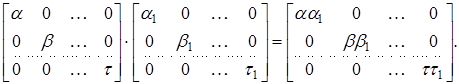
Розглянемо тепер довільну квадратну матрицю Х порядка п з елементами з кільця К. За означенням вважаємо

Оскільки при множені декількох матриць дужки можна розташовувати довільно, то для будь-яких цілих невід’ємних p, q та довільної матриці Х над асоціативним кільцем К маємо

, (2)

.

Матриці А і В називаються переставними (комутативними), якщо