Научная работа: Применение неравенств при решении олимпиадных задач
Так как точки А1 , А2 , …, Аn принадлежат надграфику выпуклой функции, то и их центр масс также принадлежит надграфику (ибо надграфик – выпуклая фигура). А это означает, что ордината центра масс М не меньше ординаты точки на графике с той же абсциссой (рис. 1), т.е.
 . (2)
. (2)
 |
???. 1
Для завершения доказательства остаётся положить m1 = α1 , …, mn = αn .
Однако есть два важных замечания. Во-первых, в процессе доказательства неравенства Йенсена (1) мы доказали неравенство (2). На самом деле эти неравенства равносильны. Положив в неравенстве (1)  (i=1, 2, ..., n), мы получаем неравенство (2). Поэтому естественно эти два неравенства называются неравенствами Йенсена. Неравенство (1) выглядит более компактно, однако для приложений удобней пользоваться неравенством (2). Во-вторых, если функция
(i=1, 2, ..., n), мы получаем неравенство (2). Поэтому естественно эти два неравенства называются неравенствами Йенсена. Неравенство (1) выглядит более компактно, однако для приложений удобней пользоваться неравенством (2). Во-вторых, если функция ![]() вогнутая, то для неё неравенства Йенсена (1) и (2) меняются на противоположные. Чтобы доказать это, достаточно рассмотреть выпуклую функцию
вогнутая, то для неё неравенства Йенсена (1) и (2) меняются на противоположные. Чтобы доказать это, достаточно рассмотреть выпуклую функцию ![]() .
.
Неравенство Коши-Буняковского
На первый взгляд, неравенство Йенсена не производит особого впечатления: слишком общо выглядит формулировка. Однако дальше можно убедиться, что это впечатление обманчиво.
Продемонстрировать силу неравенства Йенсена можно на конкретном примере. А именно, доказать знаменитое неравенство Коши-Буняковского ![]() , где a1 , a2 , …, an , b1 , b2 , …, bn – произвольные положительные числа.
, где a1 , a2 , …, an , b1 , b2 , …, bn – произвольные положительные числа.
Доказательство:
Как мы знаем, функция ![]() - выпуклая. Напишем для этой функции неравенство Йенсена (2):
- выпуклая. Напишем для этой функции неравенство Йенсена (2):
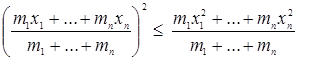 , (mi >0).
, (mi >0).
Следовательно, ![]() . Положив
. Положив 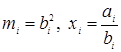 , получим требуемое неравенство.
, получим требуемое неравенство.
Неравенство Коши
При решении многих задач часто используется классическое неравенство Коши о среднем арифметическом и среднем геометрическим неотрицательных чисел.
Пусть x1 , x 2 , …, xn – неотрицательные числа. Средним арифметическим этих чисел называется число –
![]() .
.
Средним геометрическим чисел x1 , x 2 , …, xn называется число –
![]() .
.
Теорема 1. Если x1 , x 2 , …, xn – неотрицательные числа, то имеет место неравенство
![]() . (1)
. (1)
Причём знак равенства в нем достигается тогда и только тогда, когда все числа равны.
Соотношение (1) называется неравенством Коши. При n=2 неравенство Коши следует из очевидного неравенства
![]() . Действительно,
. Действительно, ![]() , откуда
, откуда
![]() . (2)
. (2)
Отметим, что знак равенства в (2) имеет место тогда и только тогда, когда x1 =x2 .
Пусть x1 , x 2 , …, xn – положительные числа. Средним гармоническим (средним пропорциональным) этих чисел называется число –
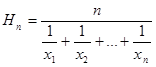 .
.
Теорема 2. Если x1 , x 2 , …, xn – положительные числа, то имеют место неравенства
An ≥Gn ≥ Hn .
Действительно, применяя к числам ![]() неравенство Коши, получаем
неравенство Коши, получаем