Научная работа: Применение неравенств при решении олимпиадных задач

Умножим его на неотрицательное число 1+x_{n +1} (оно неотрицательно, т.к. ). Получим:

.

Т.к. x_i одного знака, произведения в правой части положительны, и если их отбросить, неравенство только усилится. Получаем:

.

Как мы видим, неравенство верно и для n+1 членов, а значит верно для любых n.

Доказательство(II способ):

Также применяем метод математической индукции.

При n=1 имеем , . Утверждаем, что при n=k неравенство верно: . Тогда при n=k+1 имеем

.

Неравенство доказано.

Весовое (общее) неравенство Коши

Ранее мы рассмотрели так называемое классическое неравенство Коши. Однако очень большое значение имеет также одно важное обобщение неравенства Коши – это общее, или весовое, неравенство Коши.

Теорема. Для любых действительных положительных чисел m₁ , m₂ , …, m_n и для любых неотрицательных x₁ , x₂ , …, x_n имеет место неравенство

. (1)

Числа m₁ , m₂ , …, m_n называются весовыми коэффициентами.

Неравенство (1) выполняется и для неотрицательных весовых коэффициентов m₁ , m₂ , …, m_n , но в этом случае необходимо требовать, чтобы знаменатель левой части (1) не превращался в ноль и выражения имели смысл (т.е. не все m₁ , m₂ , …, m_n равны нулю и числа x_i и m_i одновременно не равнялись нулю).

Понятно, что при m₁ = m₂ = …= m_n , весовое неравенство Коши превращается в обыкновенное неравенство Коши.

Выражение, которое стоит в левой части (1), называется весовым средним арифметическим, а то, которое в правой – весовым средним геометрическим.

Неравенство (1), для натуральных m₁ , m₂ , …, m_n , непосредственно следует из обыкновенного неравенства Коши:

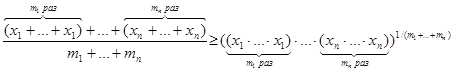. (2)

Неравенство (1) с неотрицательными рациональными весовыми коэффициентами легко привести к случаю, когда .

3.2 Решение задач с применением данных неравенств

Неравенство Йенсена

Задача:

Пусть a₁ ,…, a_n > 0, . Доказать .

Решение:

Записываем неравенство Йенсена для f(x)=x² , m_i =n. Получаем:

, , ,

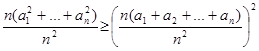что и требовалось доказать.

Неравенство Коши-Буняковского