Реферат: Билеты математические методы исследования экономики
5) Дать определение уравнения Беллмана.
6) Для матрицы А = 
найти 3А.
7) Проверить, является ли функция f(x,y) = 100 x1/4 y3/4 однородной, и если да, определить - какой степени.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ЭКОНОМИКИ
Билет № 11
1) Привести запись системы линейных уравнений в матричном виде.
2) Привести постановку задачи о рационе.
3) Дать определение вогнутой функции двух переменных.
4) Абсолютное приращение функции двух переменных по переменной у.
5) Какие методы называются методами спуска?
6) В игре двух лиц с нулевой суммой матрица выигрышей Н:
Н =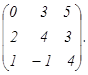 
Найти решение игры.
7) Вычислить абсолютное приращение функции f(x,y) = 20xy при движении по направлению у = 2 х из точки М (1,2), если переменная х увеличивается на единицу.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ЭКОНОМИКИ
Билет № 12
1) Дать понятие обратной матрицы.
2) Привести экономический смысл превращения некоторого ограничения прямой задачи на оптимальном плане в строгое неравенство, считая, что решается задача составления плана производства.
3) Возрастание функции z = f(x,y) по переменой х.
4) Абсолютное приращение функции двух переменных по переменной х.
5) Участники задачи принятия решений.
6) Для матриц А = 
и В = 
найти 2А + 3В.
7) Найти градиент функции f(x,y) = 15 x1/3 y2./3 в точке (27,8).
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ЭКОНОМИКИ
Билет № 13
1) Привести свойства скалярного произведения векторов.
2) Дать понятие опорного плана в задаче линейного программирования.
3) В игре двух лиц с нулевой суммой привести величину среднего выигрыша Игрока 1, если Н – матрица выигрышей, х, у – смешанные стратегии Игроков 1 и 2.
4) Градиент и необходимые условия экстремума функции двух переменных.
5) Привести связь задачи выпуклого программирования и функции Лагранжа.
6) В игре двух лиц с нулевой суммой привести пример чистой стратегии Игрока 2, если матрица выигрышей Н равна
Н =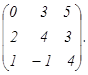
7) Для функции f(x,y) = 10х + 15у описать и построить линию уровня:
30х + 15у = 210.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ЭКОНОМИКИ
Билет № 14
1) Привести правило определения размерности матрицы, являющейся произведением матриц А и В.
2) Сформулировать условие, связанное с тем, что на оптимальном плане некоторое ограничение прямой задачи линейного программирования, например i-ое, выполняется как строгое неравенство.
3) Понятие глобального максимума функции двух переменных.
4) Линейная функция двух переменных и ее график.
5) Привести необходимые и достаточные условия существования седловой точки для функции L(x,y), вогнутой по переменной х и выпуклой по переменной у ( L(x,y) - функция двух переменных ).