Реферат: Билеты математические методы исследования экономики
7) Указать область определения функции: f(x,y) = 10 x1/4 y3/4
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ЭКОНОМИКИ
Билет № 15
1) Привести решение системы линейных уравнений методом Гаусса.
2) Сформулировать условие, связанное со строгой положительностью некоторой координаты, например уi *, оптимального решения двойственной задачи линейного программирования.
3) Что является предметом теории игр?
4) Относительное приращение функции двух переменных по переменной х.
5) Дать определение множителей Лагранжа.
6) Найти произведение матриц А = 
и В = 
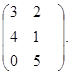
7) Вычислить значение функции f (x1 , x2 , x3 , x4 ) = 8 x1 x2 + 4
+ 10 x1 (x4 )2 в точке (1, 2, 4, 3)
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ЭКОНОМИКИ
Билет № 16
1) Объяснить связь базиса и размерности пространства.
2) Дать основные положения задачи линейного программирования.
3) В игре двух лиц с нулевой суммой дать понятие оптимальной стратегии Игрока 1.
4) Дать понятие стационарной точки функции двух переменных.
5) Дать геометрическую интерпретацию метода наискорейшего спуска в случае максимизации функции двух переменных.
6) Для матрицы А = 
найти транспонированную и указать ее размерность.
7) Найти частную производную первого порядка по у функции
f(x,y) =20xy.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ЭКОНОМИКИ
Билет № 17
1) Привести способ вычисления определителя путем разложения его по строке.
2) Привести двойственную задачу для следующей задачи линейного программирования: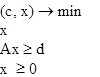
Каковы размерности двойственной задачи линейного программирования, если прямая задача имеет размерности: векторы х и р размерности n, вектор в – размерности m, матрица А – размерности m х n?
3) В игре двух лиц с нулевой суммой привести понятие нижней цены игры.
4) Относительное приращение функции двух переменных по переменной у.
5) Описать метод наискорейшего спуска.
6) Решить систему неравенств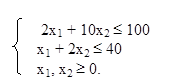 
7) Для функции f (x,y) = (x - 3)2 + ( y - 4)2 в точке (5,4) построить градиент и линию уровня, проходящую через эту точку. Решение изобразить геометрически.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ЭКОНОМИКИ
Билет № 18
1) Дать понятие вектора n-мерного пространства. Привести пример вектора 4-мерного пространства.
2) Привести запись двойственных друг другу задач в матричной форме.
3) Убывание функции z = f(x,y) по переменной у.
4) Понятие антиградиента функции нескольких переменных.
5) Что изучает раздел стохастического программирования?
6) Решить систему уравнений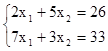 
7) Проверить на выпуклость множества, точки которого являются решением неравенства (можно геометрически): {(x,y): x2 + y2 £ 100}.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ЭКОНОМИКИ
Билет № 19