Реферат: Численные методы решения систем линейных алгебраических уравнений
: 
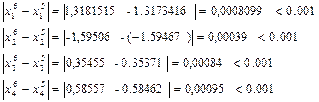
Необходимая точность достигнута на 6-й итерации. Таким образом, итерационный процесс можно прекратить [14].
2.3 Метод Зейделя
2.3.1 Описание метода
В этом методе результаты, полученные на k-том шаге, используются на этом же шаге. На (k+1) - й итерации компоненты приближения 
вычисляются по формулам:
………………………………………….
Этот метод применим к система уравнений в виде Ax=B при условии, что диагональный элемент матрицы коэффициентов A по модулю должен быть больше, чем сумма модулей остальных элементов соответствующей строки (столбца).
Если данное условие выполнено, необходимо проследить, чтобы система была приведена к виду, удовлетворяющему решению методом простой итерации и выполнялось необходимое условие сходимости метода итераций:
, либо 
2.3.2 Решение СЛАУ методом Зейделя
Решить СЛАУ методом Зейделя с точностью 
.
Эту систему можно записать в виде:
В этой системе сразу видно, что выполняется условие, где диагональные элементы матрицы коэффициентов по модулю больше, чем сумма модулей остальных элементов соответствующей строки.
Для удобства преобразуем систему к виду:
Условие сходимости: