Реферат: Численные методы решения систем линейных алгебраических уравнений

x₁₌ 0+ c₁₂ x₂ + c₁₃ x₃ -…+ c_{1 n -1} x_{n -1} + c_{1 n} x_n +d₁

x₂₌ c₂₁ x₂ +0 +c₂₃ x₃ +…+ c_2n-1 x_n-1 + c_2n x_n +d₂

_{………………………………………………………. .}

x_n= c_n1 x₁ + c_n2 x₂ +c_n3 x₃ +…+ c_nn-1 x_n-1 + 0+d_n

В ней на главной диагонали матрицы С находятся нулевые элементы, остальные элементы выражаются по формулам:

с_ij =-a_ij /a_ii , d_i =c_i /a_ii (i,j=1,2,3…n, i<>j)

Итерационный процесс продолжается до тех пор, пока значения х₁ ^{( k ),} х₂ ^{( k ),} х₃ ^{( k )} не станут близкими с заданной погрешностью к значениям х₁ ^{( k -1),} х₂ ^{( k -1),} х₃ ^{( k -1).}

2.2.2 Решение СЛАУ методом простых итераций

Решить СЛАУ методом простых итераций с точностью .

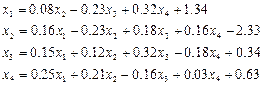
Для удобства преобразуем систему к виду:

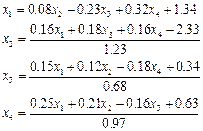
Условие сходимости:

,

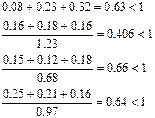
Принимаем приближение на 0-ом шаге:

,

,

На 1-м шаге выполняем следующее:

Подставляем принятые приближения в первоначальную систему уравнений

Смотрим не выполняется ли условие остановки итерационного процесса:

:

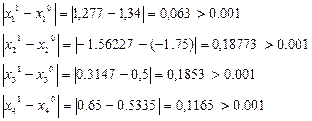
На 2-м шаге выполняем следующее: