Реферат: Экзаменационные билеты по аналитической геометрии за первый семестр 2001 года

59. При каком значении a прямая будет лежать на плоскости 3x – y – z – 3 = 0?

60. Найти координаты вектора, представляющего собой векторное произведение вектора = (1, 6, 0) и вектора (1, -1, -1).

61. Найти общее уравнение плоскости, проходящей через ось Оу и точку М (3, 0, 2).

62. Найти общее уравнение плоскости, проходящей через ось Оy и точку М(3, 0, 2).

63. Написать общее уравнение плоскости, проходящей через начало координат.

64. Написать общее уравнение плоскости, проходящей через ось Оу.

65. Найти направляющий вектор прямой: .

66. Найдите уравнение плоскости, проходящей через три данные точки: М₁ (0, 0, 0), М₂ (2, -1, 2), М₃ (0, -1, 1).

67. С помощью определителя третьего порядка найти смешанное произведение трех векторов = (1, 2, 3), = (-1, 2, 4), = (1, 1, 0).

68. Меридиан 4x² - z² = 4 вращается вокруг оси Оz. Какая поверхность второго порядка при этом получается?

69. Меридиан 2y = x² вращается вокруг оси Оy. Какая поверхность второго порядка при этом получается?

70. Меридиан = -1 вращается вокруг оси Оz. Какая поверхность второго порядка при этом получается?

71. Меридиан x² + z² = 16 вращается вокруг оси Оz. Какая поверхность второго порядка при этом получается?

72. Докажите, что прямая лежит на гиперболоиде .

73. Найдите точки пересечения прямой: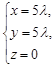 и сферы х² + у² + z² = 100.

74. С помощью какого преобразования координат приводится к каноническому виду уравнение поверхности второго порядка ? Как называется эта поверхность?

75. Какие плоскости симметрии имеет гиперболоид ?

76. По характеристическим числам соответствующей квадратичной формы выяснить, какую невырожденную поверхность второго порядка определяет следующее уравнение: 4x² – y² – z² – 4xz =2?

77. По характеристическим числам соответствующей квадратичной формы выяснить, какую невырожденную поверхность второго порядка определяет следующее уравнение: 5x² + 2y² + z² + 2xz = 5?

78. Приведите к каноническому виду уравнение поверхности второго порядка 5x² + 2y² + 7z² – 4yx = 42. Определить вид этой поверхности.

79. Приведите к каноническому виду уравнение поверхности второго порядка 8x² + 2y² + 5z² + 4yz = 48. Определить вид этой поверхности.

80. Приведите к каноническому виду уравнение поверхности второго порядка x² + y² + 2z² – 8xy – 6xz + 24 = 0. Определить вид этой поверхности.

Экзаменационный билет по предмету

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

Билет № 1

1. Какое число называется смешанным произведением трех векторов , , ?

2. С помощью определителя третьего порядка найти смешанное произведение трех векторов = (1, 1, 3), = (-1, 0, 4), = (2, 1, 0).

3. Перечислите вырожденные поверхности второго порядка.

4. Как называется линия второго порядка, по которой плоскость
х = 1 пересекает гиперболоид + у² - z² = 1? Напишите уравнение этого сечения.

5. Приведите к каноническому виду уравнение поверхности второго порядка:
х² + 3у² - z² + 6zу - 4 = 0.

Зав. кафедрой

--------------------------------------------------

Экзаменационный билет по предмету

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

Билет № 2

1. Как вычисляется определитель третьего порядка ?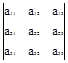
Вычислить определитель третьего порядка .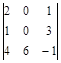

2. Найти координаты точки пересечения прямых у = 5х - 4 и .