Реферат: Экзаменационные вопросы и билеты по предмету МАТЕМАТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ЭКОНОМИКИ за весенний семестр 2001 года

30. Задача нелинейного программирования. Постановка.

31. Понятие выпуклых функций и выпуклых множеств. Задача выпуклого программирования. Постановка. Свойства.

32. Схема градиентных методов решения задачи выпуклого программирования. Метод наискорейшего спуска.

33. Функция Лагранжа задачи выпуклого программирования. Множители Лагранжа.

34. Условия Куна-Таккера.

35. Задача динамического программирования.

36. Метод динамического программирования. Принцип оптимальности Боллмана. Область применения динамического программирования.

37. Задача стохасического программирования в жесткой постановке и по средним.

38. Задачи экономики.

39. Постановка задачи принятия решения. Участники задачи принятия решения.

40. Методы обработки экспертной информации.

41. Для векторов x = (1, 0, 2, 4, 7), y = (0, 2, 4, 1, 1) указать размерность, построить векторы 2x, 5y, 3x + 2y, вычислить (x, y), (3x, 2y), (2x + y, x + 2y).

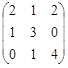42. Для матриц А = , В = найти А + В, 3А + 4В, В', А·В, В·А, |A|, A^-1 .

43. Систему уравнений записать в матричной форме: . Решить.

44. Решить задачу линейного программирования: 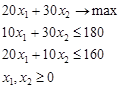. Указать оптимальное решение (x₁ , x₂ ), максимальное решение целевой функции 20x₁ + 30x₂ . Построить двойственную и найти ее решение. Дать геометрическую иллюстрацию, интерпретацию условий двойственности.

45. В игре двух лиц с нулевой суммой с матрицей выигрышей Н = 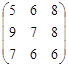указать: ― число стратегий первого игрока; ― вторую стратегию сторого игрока; ― нижнюю цену игры; ― верхнюю цену игры.

46. Для функции Z = найти: ― значение функции в точке (32, 243); ― частные производные первого и второго порядков по x и по y в точке (32, 243).

47. Для функции Z = 60xy найти: ― абсолютное и относительное приращения функции при переходе из точки (1, 2): в точку (1, 4), в точку (5, 2), по направлению y = 3x при ∆x = 2.

48. Обосновать выпуклость множеств, заданных условиями: 1) ; 2) ; 3) ; 4) ; 5) .

49. Проверить, является ли функция выпуклой (вогнутой): 1) ; 2) ; 3) ; 4) .

50. Построить график функции в точке: 1) ƒ(x, y) = (x - 1)² + (y - 3)² в точке (4, 7); 2) ƒ(x, y) = 20x + 18y в точке (1, 1); 3) ƒ(x, y) = 80xy в точке (3, 1); 4) ƒ(x, y) = 45x^½ y^½ в точке (9, 16).

51. Построить функцию Лагранжа для задачи при условиях: 3x + 8y ≤ 48 x, y ≥ 0.

52. Решить задачу стохастического программирования в постановке “по срезам”: 5x + 3y → max 4x + 6y ≤ b x, y ≥ 0. b принимает значение 18 с вероятностью и значение 45 с вероятностью .

Экзаменационный билет по предмету

МАТЕМАТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ЭКОНОМИКИ

Билет № 1

1) Показать результат произведения матрицы размерности m х n на вектор-столбец.

2) Привести двойственную задачу для следующей задачи линейного программирования:

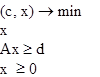
Каковы размерности двойственной задачи линейного программирования, если прямая задача имеет размерности: векторы х и р размерности n, вектор в – размерности m, матрица А – размерности m х n?

3) Понятие глобального максимума функции двух переменных.

4) Экономический смысл отрицательности частной производной первого порядка по х функции двух переменных.

5) Описать метод наискорейшего спуска.

6) Предприятие выпускает два вида продукции, используя один вид сырья. Для производства единицы продукции каждого вида требуется 30 ед. и 20 ед. сырья, соответственно. Цена сырья – 300 руб./ед. Определить стоимость сырья, необходимого для осуществления следующего выпуска продукции .