Реферат: Экзаменационные вопросы и билеты по предмету МАТЕМАТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ЭКОНОМИКИ за весенний семестр 2001 года
31) Возрастание функции z = f(x,y) по переменой х.
32) Свойство отрицательности частной производной первого порядка по х функции двух переменных (
).
33) Функция Лагранжа для задачи выпуклого программирования.
34) Найти произведение матриц хАу, если х = (1 4), А = 
у = 
35) Найти частную производную первого порядка по х функции
f(x,y) = 10 x1/4 y3/4 .
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ЭКОНОМИКИ
Билет № 7
36) Дать понятие линейной зависимости системы векторов.
37) Сформулировать свойства допустимых планов двойственных задач линейного программирования.
38) Что такое принцип классификации по свойствам функций выигрыша (платежных функций)?
39) Показать связь производной по направлению и частных производных первого порядка функции двух переменных.
40) Дать описание ИМА.
41) Для матрицы А = 
найти транспонированную и указать ее размерность.
42) Вычислить абсолютное приращение функции f(x,y) = 20xy при переходе из точки М (3,4) в точку (3.5,4).
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ЭКОНОМИКИ
Билет № 8
43) Привести свойство матриц, имеющих определитель, не равный нулю.
44) Привести количественное значение роста выручки при уi * > 0 (уi * - i-я компонента оптимального плана двойственной задачи, прямая задача – задача составления плана производства).
45) Каковы способы классификации игр?
46) Частные производные высших порядков функции нескольких переменных.
47) Привести постановку задачи стохастического программирования "по средним".
48) В игре двух лиц с нулевой суммой матрица выигрышей Н равна:
Н = 
Чему равна нижняя цена игры?
49) Вычислить абсолютное приращение функции f(x,y) = 20xy при движении по направлению у = 2 х из точки М (1,2), если переменная х увеличивается на единицу.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ЭКОНОМИКИ
Билет № 9
50) Дать определение умножения матрицы на число.
51) Привести запись двойственных друг другу задач в матричной форме.
52) Что является предметом теории игр?
53) Свойство отрицательности частной производной первого порядка по у функции двух переменных (
).
54) Задача динамического программирования.
55) В игре двух лиц с нулевой суммой матрица выигрышей Н:
Н =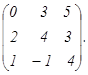 
Найти решение игры.
56) Найти частную производную первого порядка по у функции
f(x,y) =12xy2 + х + 4х3 у - 3.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ЭКОНОМИКИ
Билет № 10
57) Сформулировать основные свойства базиса пространства.
58) Записать в общем виде задачу линейного программирования на максимум в стандартной форме, если размерность задачи: две переменных, одно ограничение.
59) Область определения функции нескольких переменных.