Реферат: Экзаменационные вопросы и билеты по предмету МАТЕМАТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ЭКОНОМИКИ за весенний семестр 2001 года
91) Указать область определения функции: f(x,y) = 20 x y.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ЭКОНОМИКИ
Билет № 15
92) Дать определение алгебраического дополнения матрицы.
93) Записать общую задачу линейного программирования на максимум в стандартной форме с помощью матриц.
94) Понятие локального максимума функции двух переменных.
95) Частная производная первого порядка по у функции двух переменных.
96) Дать определение множителей Лагранжа.
97) В игре двух лиц с нулевой суммой матрица выигрышей Н равна:
Н = ![]() Привести пример смешанной стратегии Игрока 2.
Привести пример смешанной стратегии Игрока 2.
98) Найти частную производную первого порядка по у функции
f(x,y) = 10 x1/4 y3/4 .
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ЭКОНОМИКИ
Билет № 16
99) Дать понятие базиса n-мерного пространства.
100) Сформулировать условие, связанное с тем, что на оптимальном плане некоторое ограничение прямой задачи линейного программирования, например i-ое, выполняется как строгое неравенство.
101) В игре двух лиц с нулевой суммой привести понятие смешанной стратегии.
102) Понятие градиента функции двух переменных.
103) Привести формулировку задачи пошаговой оптимизации.
104) Для задачи линейного программирования
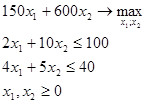
Привести пример допустимого плана двойственной задачи
105) Для следующей задачи выпуклого программирования
f(x,y) = (x1 - 5)2 + (x2 - 6)2 -> max при ограничениях:
![]()
построить функцию Лагранжа.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ЭКОНОМИКИ
Билет № 17
106) Привести свойства скалярного произведения векторов.
107) Дать основные положения задачи линейного программирования.
108) В игре двух лиц с нулевой суммой дать понятие оптимальной стратегии Игрока 1.
109) Относительное приращение функции двух переменных по переменной х.
110) Приведите схему решения задачи выпуклого программирования с помощью градиентных методов.
111) Задачу линейного программирования записать в матричном виде: 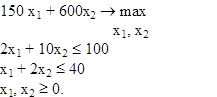
112) Для функции f(x,y) = 10х + 15у описать и построить линию уровня: 30х + 15у = 210.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ЭКОНОМИКИ
Билет № 18
113) Дать правило расчета определителя матрицы размерности 2 х 2.
114) Привести свойства решения задачи линейного программирования.
115) Дать геометрическую интерпретацию выпуклости функции одной переменной.
116) Необходимые условия экстремума функции двух переменных.
117) Свойства задачи выпуклого программирования.
118) Для задачи линейного программирования
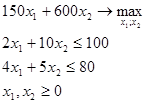
Изобразить геометрически множество допустимых планов двойственной задачи.
119) Вычислить значение функции f(x,y) = 20 x y в точке (3,4).
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ЭКОНОМИКИ
Билет № 19