Реферат: Интеграл и его применение

Теорема. Если f(x) непрерывная и неотрицательная функция на отрезке [a;b], то площадь соответствующей криволинейной трапеции равна приращению первообразных.

Дано: f(x)– непрерывная неопр. функция, xÎ[a;b].

Доказать: S = F(b) – F(a), где F(x) – первообразная f(x).

Доказательство:

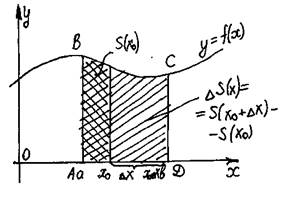1) Рассмотрим вспомогательную функцию S(x). Каждому xÎ[a;b] поставим в соответствие ту часть криволинейной трапеции, которая лежит левее прямой, проходящей через точку с этой абциссой и параллельно оси ординат. Следовательно S(a)=0 и S(b)=Sтр

Докажем, что S(a) – первообразная f(x).

D( f ) = D(S) = [a;b]

S’(x0)= lim( S(x0+Dx) – S(x0) / Dx ), при Dx®0 DS – прямоугольник

Dx®0 со сторонами Dx и f(x0)

S’(x0) = lim(Dxf(x0) /Dx) = limf(x0)=f(x0): т.к. x0 точка, то S(x) –

Dx®0 Dx®0 первообразная f(x).

Следовательно по теореме об общем виде первообразной S(x)=F(x)+C.

Т.к. S(a)=0, то S(a) = F(a)+C

C = –Fa

S = S(b)=F(b)+C = F(b)–F(a)

II.

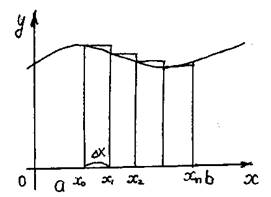1). Разобьем отрезок [a;b] на n равных частей. Шаг разбиения Dx=(b–a)/n. При этом Sтр=lim(f(x0)Dx+f(x1)Dx+...+f(xn))Dx= n®¥ = lim Dx(f(x0)+f(x1)+...+f(xn)) При n®¥ получим, что Sтр= Dx(f(x0)+f(x1)+...+f(xn))

Предел этой суммы называют определенным интегралом.

b

Sтр=òf(x)dx

a

Сумма стоящая под пределом, называется интегральной суммой.

Определенный интеграл это предел интегральной суммы на отрезке [a;b] при n®¥. Интегральная сумма получается как предел суммы произведений длины отрезка, полученного при разбиении области определения функции в какой либо точке этого интервала.

a — нижний предел интегрирования;