Реферат: Интеграл и его применение
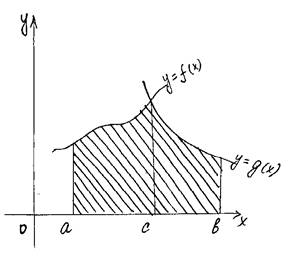
b b
S= ò f(x)dx = ò g(x)dx
a a
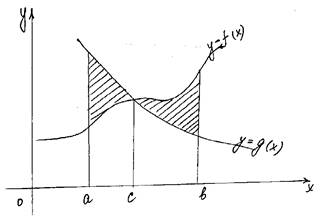 |
c b S = ò (f(x)–g(x))dx+ò(g(x)–f(x))dx a c |
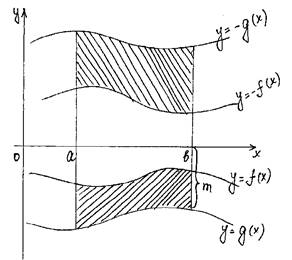 |
f(x)® f(x)+m g(x)®g(x)+m b S= ò (f(x)+m–g(x)–m)dx = a b = ò (f(x)– g(x))dx a Если на отрезке [a;b] f(x)³g(x), то площадь между этими графиками равна b ò ((f(x)–g(x))dx a |
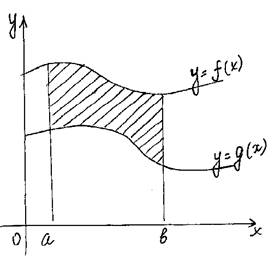 |
Функции f(x) и g(x) произвольные и неотрицательные b b b S=ò f(x)dx – ò g(x)dx = ò (f(x)–g(x))dx a a a |
|
|
b b S=ò f(x)dx + ò g(x)dx a a |
Применение интеграла
I. В физике.
Работа силы (A=FScosa, cosa¹ 1)
Если на частицу действует сила F, кинетическая энергия не остается постоянной. В этом случае согласно