Реферат: Интеграл и его применение
ò f(x)dx = ò f(x)dx + ò f(x)dx
a a c
F(b) – F(a) = F(c) – F(a) + F(b) – F(c) = F(b) – F(a)
(это свойство аддитивности определенного интеграла)
Если l и m постоянные величины, то
bbb
ò (lf(x) +mj(x))dx = lò f(x)dx + mòj(x))dx –
aac
– это свойство линейности определенного интеграла.
6.
b b b b
ò (f(x)+g(x)+...+h(x))dx = ò f(x)dx+ ò g(x)dx+...+ ò h(x)dx
a a a a
b
ò (f(x)+g(x)+...+h(x))dx = (F(b) + G(b) +...+ H(b)) –
a
– (F(a) + G(a) +...+ H(a)) +C =
= F(b)–F(a)+C1 +G(b)–G(a)+C2+...+H(b)–H(a)+Cn=
b b b
= ò f(x)dx+ ò g(x)dx+...+ ò h(x)dx
aaa
Набор стандартных картинок
|
|
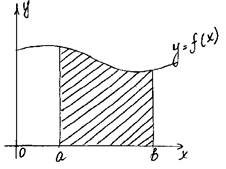
Т.к. f(x)<0, то формулу Ньютона-Лейбница составить нельзя, теорема верна только для f(x)³0. Надо: рассмотреть симметрию функции относительно оси OX. ABCD®A’B’CD b S(ABCD)=S(A’B’CD) = ò –f(x)dx a |
|
К-во Просмотров: 3904
Бесплатно скачать Реферат: Интеграл и его применение
|