Реферат: Исследование наилучших приближений непрерывных периодических функций тригонометрическими полиномами

.

В работе [3] С.Н.Бернштейн доказал также эквивалентность условий 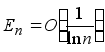и .

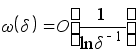Мы переносим эти теоремы на условия вида

,

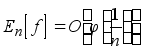где j ÎN ^a .

Кроме того, в этом параграфе доказано, например, такое предложение: пусть k - натуральное число и

;

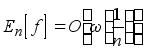для того, чтобы , необходимо и достаточно выполнение условия

.

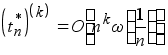В конце параграфа даются уточнения теорем Валле-Пуссена.

В §7 доказывается основная теорема. Мы даём здесь же оценку E_n [f ] снизу, если

.

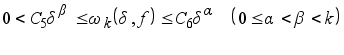Именно, тогда

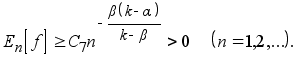
Случай a =0 установлен С.Н.Бернштейном [3].

В §8 мы рассматриваем несколько решений задач с использованием различных модулей непрерывности.

§1. Некоторые вспомогательные определения.

В работе рассматриваются непрерывные функции f с периодом 2p и их приближение тригонометрическими полиномами. Через t_n (x )обозначается тригонометрический полином порядка не выше n , а через t_n ^* (x )=t_n ^* (x,f )-тригонометрический полином, наименее уклоняющийся от f среди всех t_n (x) . Мы полагаем и пишем

Введём ряд определений.

Определение 1. При каждом фиксированном классом Липшица порядка a называется множество всех непрерывных функция f , модуль непрерывности каждой из которых удовлетворяет условию

где С₈ -какая-нибудь положительная постоянная, которая не зависит от d и которая, вообще говоря, является различной для разных функций. Этот класс обозначается H ^a или Lip a .

Определение 2. Обозначим при фиксированном натуральном r через W^(r) L класс функций f , которая имеет абсолютно непрерывные производные до (r- 1) порядка и у которой r -я производная принадлежит классу L .

Определение 3. Для непрерывной на [a,b ] функции f (x )назовём модулем непрерывности первого порядка или же просто модулем непрерывности функцию w (d )= w (f; d ), определённую на [0, b-a ] при помощи следующего равенства:

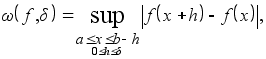(1.1)

или, что то же самое,

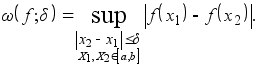(1.1’)

Свойства модуля непрерывности :