Реферат: Исследование наилучших приближений непрерывных периодических функций тригонометрическими полиномами
2.w(d) есть функция, монотонно возрастающая;
3.w(d) есть функция непрерывная;
4.w(d) есть функция полуаддитивная в том смысле, что для любых 
и 
(1.2)
Доказательство. Свойство 1) вытекает из определения модуля непрерывности.
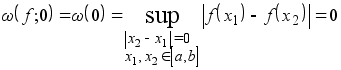
Свойство 2) вытекает из того, что при больших d нам приходится рассматривать sup на более широком множестве значений h . Свойство 4) следует из того, что если мы число 
представим в виде h=h1 +h2 , 
и 
, то получим
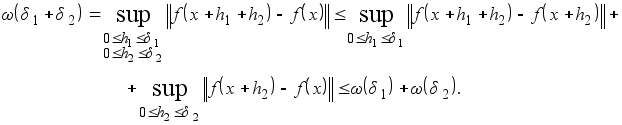
Из неравенства (1.2) вытекает, что если 
то 
т.е.
(1.3)
Теперь докажем свойство 3). Так как функция f (x ) равномерно непрерывна на [a,b ], то 
при 
и, следовательно, для любыхd, 
при 
а это и означает, что функция w ( d ) непрерывна.
Определение 4. Пусть функция f (x )определена на сегменте [a,b ]. Тогда для любого натурального k и любых 
и h>0 таких, что 
k-й разностью функции f в точке x с шагом h называется величина
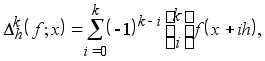(1.4)
а при 
и h>0 таких, что 
k-й симметричной разностью - величина
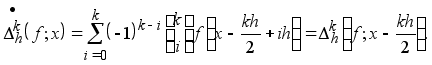(1.4’)
Лемма 1. При любых натуральных j и k справедливо равенство
(1.5)
Доказательство. Действительно, так как при любом натуральном k
то
Лемма доказана.
Лемма 2. При любых натуральных k и n верна формула:
(1.6)
Доказательство. Воспользуемся индукцией по k . При k= 1 тождество (1.6) проверяется непосредственно:
.
Предполагая его справедливость при k- 1 (k ³2), получим