Реферат: Исследование наилучших приближений непрерывных периодических функций тригонометрическими полиномами

A₁ -const . Неравенства (1.16) и (1.16‘) равносильны условию, что и требовалось доказать.

§2. Простейшие свойства модулей нерперывности.

Этот параграф носит вспомогательный характер. Здесь устанавливается несколько простейших свойств модуля нерперывности высших порядков. Все рассматриваемые здесь функции f₁ , f₂ , ... - непрерывны.

ЛЕММА 1. Для любого натурального k и любого d ³0

(2.1)

Доказательство: по определению,

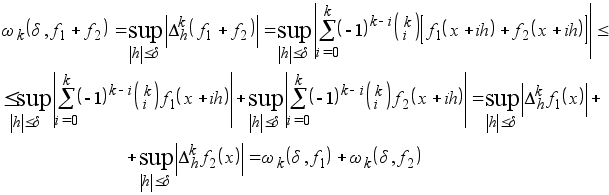
Лемма доказана.

ЛЕММА 2. Пусть f и l -натуральные числа, l Тогда для любого d ³0

(2.2)

и

(2.3)

Доказательство: Положим

Тогда для 0£l имеем

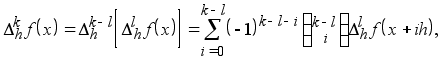
откуда

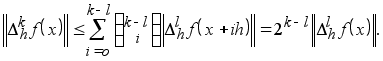
Отсюда при l =0 вытекает, что

,

а при 0<l <k

Полагая в (2.3) l =1, находим, что

Из этого неравенства видно, что для любого натурального k

. (2.4)

ЛЕММА 3. Для любого натурального k модуль непрерывности k -го порядка является непрерывной функцией от d .

Доказательство: Пусть Имеем