Реферат: Исследование наилучших приближений непрерывных периодических функций тригонометрическими полиномами
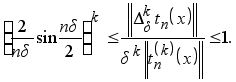 (4.3)
(4.3)
Первое неравенство совпадает с утверждением теоремы 2, а второе вытекает из оценки
![]() (4.4)
(4.4)
Таким образом, для 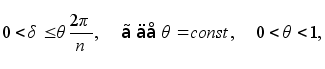 средний член в (4.3) заключен между двумя пределами, зависящими только от q .
средний член в (4.3) заключен между двумя пределами, зависящими только от q .
Следствие 2.3. Пусть ![]() . Тогда
. Тогда
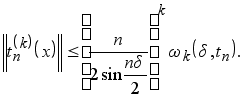 (4.5)
(4.5)
В частности,
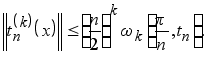 (4.6)
(4.6)
Следствие 2.4. Пусть ![]() Тогда
Тогда
![]()
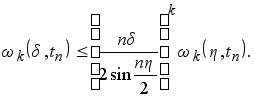 (4.7)
(4.7)
В частности, для ![]() имеем
имеем
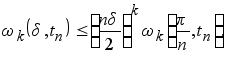 (4.8)
(4.8)
В самом деле, из (4.4) или (2.12) следует:
![]()
и остается воспользоваться неравенством (4.5).
Следствие 2.5. Пусть ![]() Тогда
Тогда
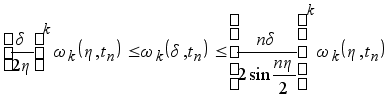 . (4.9)
. (4.9)
Вторая половина неравенства совпадает со следствием 2.4, а первая непосредственно вытекает из (2.7).
§5. Дифференциальные свойства тригонометрических полиномов, аппроксимирующих заданную функцию.
В этом параграфе устанавливается, что если тригонометрический полином tn (x ) близок к заданной функции f , то его модули непрерывности можно оценить через модули непрерывности f .
Теорема 3. Зафиксируем натуральные числа k и n и пусть
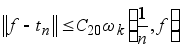 (5.1)
(5.1)
Тогда для любого ![]()
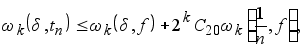 (5.2)
(5.2)
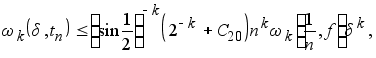 (5.3)
(5.3)
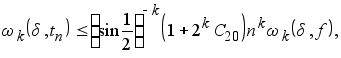 (5.4)
(5.4)
и
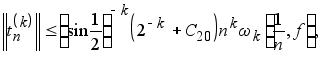 (5.5)
(5.5)
Предварительные замечания. Неравенства (5.2) и (5.4) предпочтительнее для больших d, а (5.3)-для малых. Если ![]() , то (5.2) сильнее, чем (5.4); однако (5.4) имеет более симметричную форму и часто удобнее в приложениях.
, то (5.2) сильнее, чем (5.4); однако (5.4) имеет более симметричную форму и часто удобнее в приложениях.