Реферат: Исследование наилучших приближений непрерывных периодических функций тригонометрическими полиномами

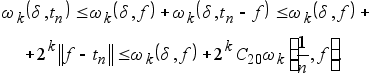
Докажем (5.5). Положим в (5.2) . Тогда получим :

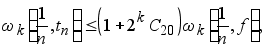
после чего (4.5) даёт (5.5).

(5.3) следует из (5.5) в силу (2.11).

Остаётся доказать (5.4). Пусть сперва . Тогда из (5.4) следует:

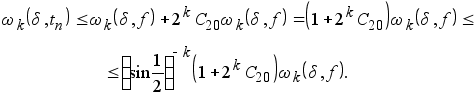
Рассмотрим, наконец, случай . Из неравенства (2.7) выводим

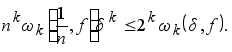
Подставляя эту оценку в (5.3), получаем (5.4) для .

Таким образом, теорема полностью доказана.

Следствие 3.1. Пусть для некоторого натурального k и любого натурального n

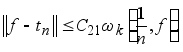(5.6)

Тогда для любого d>0

(5.7)

равномерно относительно n .

Следствие 3.2. Пусть для некоторого натурального k и любого натурального n

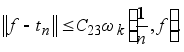
Тогда

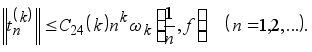(5.8)

Теорема 4. Для того, чтобы , необходимо и достаточно, чтобы

(5.9)

равномерно относительно n.

Это вытекает из теоремы 1, следствия 3.1 и того замечания что если выполнено условие (5.9), то .

Теорема 5. Для того, чтобы , необходимо и достаточно, чтобы

(5.10)

Это доказывается аналогично теореме 4, только вместо следствия 3.1 нужно воспользоваться следствием 3.2.

Неравенства теоремы 3 имеют тот недостаток, что их правые части явно зависят от константы С ₂₀ . Таким образом, если вместо фиксированного номера n и одного полинома t_n рассматривать последовательность полиномов {t_n } (n =1,2,...), то С ₂₀ окажется, вообще говоря, независящей от n и теорема 3 даёт оценки, не равномерные относительно n . Покажем как избавиться от этого неудобства.

Теорема 6. Пусть для некоторого натурального k