Реферат: Исследование наилучших приближений непрерывных периодических функций тригонометрическими полиномами
и
(5.12)
Тогда для любого d>0
(5.13)
равномерно относительно n .
Доказательство. Пусть сперва 
. Из неравенства (5.2) следует, что
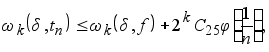
и на основании (5.11)
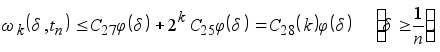(5.14)
Рассмотрим случай 
. Положим в (5.14) 
. Тогда получим
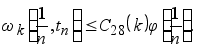
Из этого неравенства, в силу (4.7), следует, что
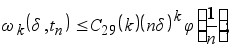
Но так как, по условию, 
, то
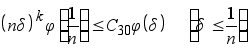
Отсюда
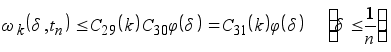
Окончательно,
и теорема доказана.
В следующем параграфе будет показано, как можно видоизменить ограничения (5.11) теоремы 6.
§6. Обобщение обратных теорем С. Н. Бернштейна и
Ш. Валле-Пуссена.
В этом параграфе обобщаются и уточняются так называемые “обратные теоремы” теории приближения. Речь идёт об оценке дифференциальных свойств функции f , если известны свойства последовательности её наилучших приближений {En }.
Лемма 9. Зададим натуральное число k , и пусть
(6.1)
и
. (6.2)
Тогда