Реферат: Исследование наилучших приближений непрерывных периодических функций тригонометрическими полиномами

Это ядро является тригонометрическим полиномом порядка n и при этом

(1.10’)

Определение 13. Ядром Фейера n -го порядка называется функция

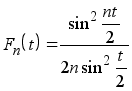(1.11)

Ядро Фейера F_n (t )является средним арифметическим первых n ядер Дирихле, и значит, является тригонометрическим полиномом порядка (n-1 ). Так что имеют место равенства

(1.11’)

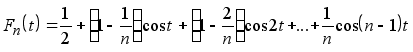(1.11’’)

где D_k (t )-ядра Дирихле.

Определение 14. Ядром Джексона n -го порядка называется функция

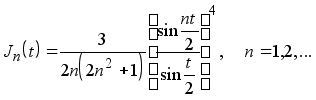(1.12)

Свойства ядер Джексона.

а) При каждом n ядро J_n (t ) является чётным неотрицательным тригонометрическим полиномом порядка 2n -2 вида

,

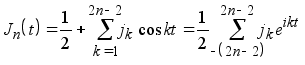где j_k =j_k (n ) - некоторые числа

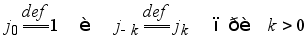
б)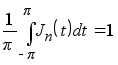

в)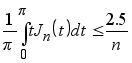

г)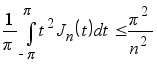

Доказательство.

а) Учитывая, что для ядер F_n (t ) Фейера имеют место равенства

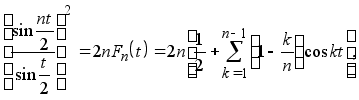получим

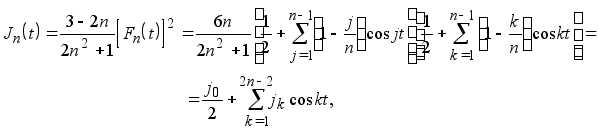
где j_k (k =1,2,...,2n -2) -некоторые числа, и в частности, в силу ортогональности тригонометрической системы функций найдем

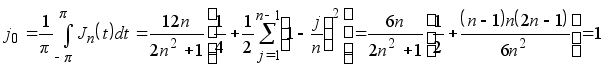
Этим свойство а) доказано.

б) Это равенство следует из равенства, полученного для j₀ .

в) Так как при любом и при 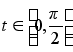(** ), то

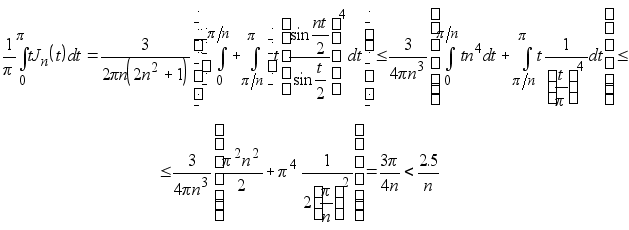
г) Совершенно аналогично случаю в) получим