Реферат: Исследование наилучших приближений непрерывных периодических функций тригонометрическими полиномами
Что и требовалось доказать.
Определение 15. Ядром типа Джексона порядка n называется функция
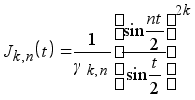, (1.13)
n =1,2,3,...,k -натуральное, где
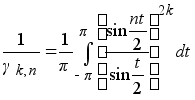(1.13’)
Ядра типа Джексона обладают следующими свойствами:
а)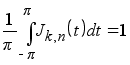 
б) При фиксированном натуральном k и произвольном n ядро Jn,k (t )
является чётным неотрицательным тригонометрическим полиномом порядка k (n -1)
в) 
n2k- 1 , т.е. существуют постоянные С14 > 0 и С15 >0, такие, что при всех n =1,2,3,... будет
г) При любом s>0 имеет место неравенство
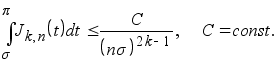
д) При любом натуральном 
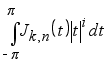
Доказательство свойств ядер типа Джексона.
а) Это свойство вытекает из равенств определения
б) Это свойство следует из 1-го неравенства определения и из того, что в силу равенств (1.11) и (1.11‘’) будет
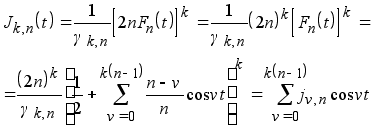(1.14)
где 
- некоторые целые числа.
в) Учитывая неравенства (**), будем иметь
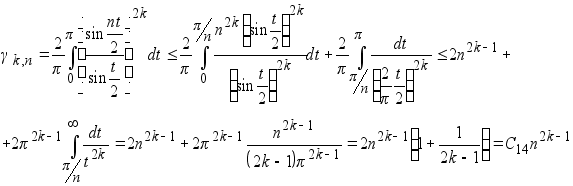(1.15)
С другой стороны
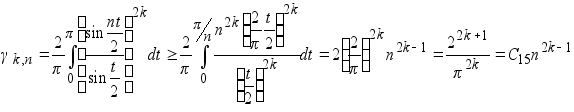(1.15‘)
г) Это неравенство вытекает из первого равенства определения и неравенства (1.15‘)
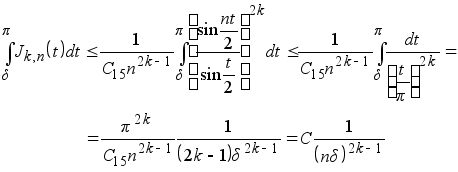
д) Действительно, с одной стороны, в силу неравенств (1.15‘) и (**)
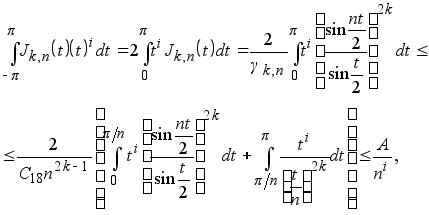(1.16)
где A-const , а с другой стороны, учитывая соотношение (1.15), неравенств (**) и из неравенства sint £t , при всех t ³0 (***), имеем