Реферат: Матрицы и определители 3

Глава 1. Матрицы………………………………………………………….7

§1. Основные определения………………………………………………..7

§2. Линейные операции над матрицами…...……………………………..8

§3. Умножение матриц………….…………………………………………8

Глава 2. Определители……………………………………………………10

§1. Определители второго и более высоких порядков……………………………………………………………………10

§2. Свойства определителей………………………………………………12

Глава 3. Обратная матрица. Существование и структура обратной матрицы…………………………………………………………………….13

Файл материалов….………………………………………………………16

Перечень умений…………………………………………………………...21

Тренинг умений…………………………………………………………….23

Задания для самостоятельной работы……………………………………………………………………….30

Глоссарий

Тематический план

Матрицы, действия над матрицами (сложение, умножение на число, умножение матриц).

Определители 2^го и 3^го порядков.

Правило Саррюса (треугольника).

Свойства определителей. Обратная матрица.

Литература

Основная

1. И.В. Виленкин, В.М. Гробер Высшая математика. Ростон-на-Дону, 2002
2. В.Е. Шнейдер, А.И. Слуцкий, А.С. Шумов Краткий курс высшей математики. Т. 1, М. 1978

Дополнительная

3. П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова Высшая математика в упражнениях и задачах. Ч. 1. М. 1980

Тематический обзор

Широкое применение математических методов в самых различных областях науки, техники, экономики и практической деятельности инженеров предъявляет повышенные требования к изучению математических приемов. Особенно важны методы и приемы линейной алгебры, наиболее простые и важные из которых рассматриваются в этом курсе.

В задачи нашего курса входит ознакомление с действиями над матрицами, изучение вычисления определителей, нахождения обратной матрицы.

Глава 1. Матрицы

§1. Основные определения.

МАТРИЦЕЙ размера m^. n называется прямоугольная таблица чисел

,

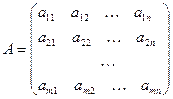содержащая m строк и n столбцов. Каждый элемент матрицы а _ik имеет два индекса: i – номер строки и k – номер столбца. Краткая форма записи матрицы:

А = (а _ik )_{m, n}

Матрица называется КВАДРАТНОЙ порядка n , если она состоит из n строк, и n столбцов.

Матрица размера 1 ^. n называется МАТРИЦЕЙ-СТРОКОЙ , а матрица размера m^. 1 - МАТРИЦЕЙ-СТОЛБЦОМ .

НУЛЕВОЙ матрицей заданного размера называется матрица, все элементы которой равны нулю.

ТРЕУГОЛЬНОЙ матрицей n-го порядка называется квадратная матрица, все элементы которой, расположенные ниже главной диагонали, равны нулю:

.

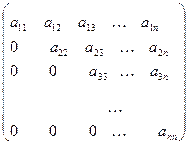ЕДИНИЧНОЙ называется квадратная матрицаn-го порядка, у которой элементы главной диагонали равны единице, а в се остальные элементы – нули:

.

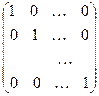Матрицы А = (а _ik )_{m, n} и В = (в _ik )_{m, n} называются РАВНЫМИ , если а _ik = в _ik i = 1,…,m

k = 1,…,n.

§2. Линейные операции над матрицами.