Реферат: Матрицы и определители 3
ПРОИЗВЕДЕНИЕМ матрицы А = (а ik )m, n на число l называется матрица lА = (lа ik )m, n .
Для любых матриц одинакового размера и любых чисел l и m выполняются свойства:
1) А + В = В +А 2) А + (В + С) = (А + В) + С
3) А + 0 = А 4) l(mА) = (lm)А
5) l(А + В) = lА + lВ 6) (l + m)А = lА + mА
Докажем свойство 5):
l(А + В) = (l(а ik + в ik ))m, n = (lа ik + lв ik )m, n = (lа ik )m, n + lв ik )m, n = lА + lВ
Доказательство Остальных свойств читатель проведет самостоятельно.
ТРАНСПОНИРОВАННОЙ для матрицы А называется матрица АТ , строки которой являются столбцами матрицы А, а столбцы – строками матрицы А.
ПРИМЕР 1. Даны матрицы
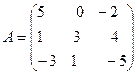и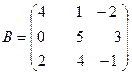 
Построить матрицу С = 2А – 3В + АТ .
РЕШЕНИЕ .
-
+
+
=
.
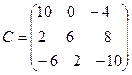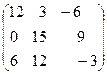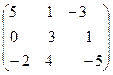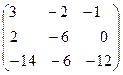§3. Умножение матриц.
ПРОИЗВЕДЕНИЕМ матрицы А = (а ik )m,р на матрицу В = (в ik )р , n называется матрица D размера m. n с элементами
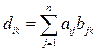
Иными словами, для получения элемента, стоящего в i -ой строке результирующей матрицы и в k -ом ее столбце, следует вычислить сумму попарных произведений элементовi -ой строки матрицы А на k -ый столбец матрицы В.
ПРИМЕР 2. Найти произведение матрицы
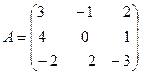на матрицу 
.
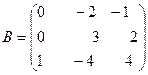РЕШЕНИЕ.
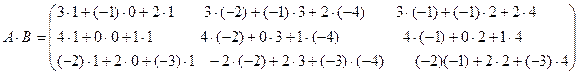
т.е.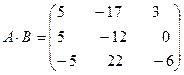 
.
В самом определении произведения матриц заложено, что число столбцов первой матрицы равно числу строк второй. Это – условие согласования матриц при умножении. Если оно нарушено, матрицы перемножить нельзя. Поэтому возможна ситуация, когда произведение А*В существует, а произведение В*А – нет. Кроме того, когда существуют оба произведения, то чаще всего они не совпадают, т.е. в большинстве случаев произведение матриц некоммутативно: А*В¹В*А. Если А, В, С – квадратные матрицы одинакового порядка и Е – единичная матрица того же размера, то справедливы тождества:
Свойство 1) оставим без доказательства ввиду его громоздкости.
Докажем 2):
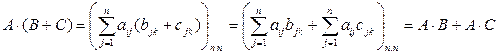
Свойство 3) доказывается аналогично, а 4) следует из определения умножения матриц.
Глава 2. Определители
§1. Определители второго и более высоких порядков.
Пусть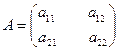 
- квадратная матрица 2-го порядка.
Определителем 2-го порядка (матрицы а) называется число