Реферат: Матрицы и определители 3
Пример . Вычислить определитель матрицы
![]() .
.
РЕШЕНИЕ . D(А) = ![]() .
.
Пусть 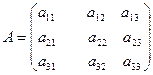 - матрица 3-го порядка.
- матрица 3-го порядка.
Определителем 3-го порядка (матрицы А) называется число
D(А) =
Правило Саррюса (треугольника)

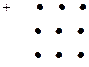
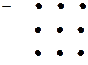
Пример . Вычислить определить
D(А) = 
Минором элемента aik называется определитель Мik , составленный из элементов, оставшихся после вычеркивания из матрицы А i -ой строки и k -го столбца.
Алгебраическим дополнением элемента aik называется число ![]() .
.
Определителем 3-го порядка (матрицы А) называется сумма произведений элементов первой строки матрицы на их алгебраические допоплнения:
D(А) =
Данную формулу называют разложением определителя по первой строке.
Пример . Вычислить определитель матрицы
 .
.
Решение . Находим миноры и алгебраические дополнения элементов 1-ой строки матрицы:

Вычисляем искомый определитель:
D(А) = 3. 7 + (-2). (-35) + 4. (-7) = 63.
Далее индуктивно вводится понятие определителей более высоких порядков.
Определителем n- го порядка называется число
 .
.
§2. Свойства определителей.
Изложенные ниже свойства справедливы для любого n- го порядка. Доказательства будем проводить для n = 3.
1. Определитель не меняется при транспонировании, т.е. D(АТ ) = D (А). Поэтому в дальнейшем большинство свойств формулируется и доказывается для строк.
2. Если две строки определителя поменять местами, то определитель меняет знак.
3. Если все элементы какой-либо строки (или столбца) равны нулю, то определитель равен нулю.
4. Если все элементы какой-либо строки (столбца) имеют общий множитель, то его можно вынести за знак определителя.