Реферат: Окружности в треугольниках и четырехугольниках
Центр окружности, вписанной в треугольник, находится на пересечении биссектрис треугольника.
Свойство: в любом описанном четырехугольнике суммы противоположных сторон равны.
Признак: если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.
2.2 Описанная окружность
Определение: если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник – вписанным в эту окружность.
Теорема: около любого треугольника можно описать окружность, и притом только одну.
Центр окружности, описанной около треугольника, находится на пересечении серединных перпендикуляров.
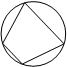
Свойство: в любом вписанном четырехугольнике сумма противоположных углов равна 180˚.
Признак: если сумма противоположных углов четырехугольника равна 180˚, то около него можно описать окружность.
2.3 Взаимное расположение прямой и окружности:
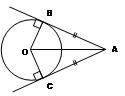
AB – касательная, если OH = r
Свойство касательной:
AB ┴ OH (OH – радиус, проведенный в точку касания H)
Свойство отрезков касательных, проведенных из одной точки:
AB = AC
ﮮ BAO = ﮮ CAO
 |

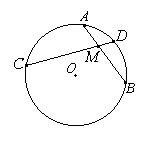
Свойство хорд: если две хорды окружности, AB и CD пересекаются в точке M, то произведение отрезков одной хорды равно произведению отрезков другой хорды: AM ∙ MB = CM ∙ MD.
Медиана
Медиана (от лат. mediana — средняя), отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
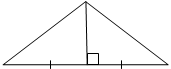
Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.
Теорема: сумма углов треугольника равна 180°