Реферат: Окружности в треугольниках и четырехугольниках
8. SBOC = 2 ∙ SBOK = 2 ∙ 20 = 40
Ответ: SBOC = 40
3.2 Задачи с окружностью, вписанной в треугольник
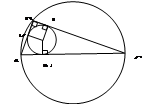
Задача 4: радиус окружности, вписанной в прямоугольный треугольник, равен 2 м, а радиус описанной окружности равен 5 м. Найдите больший катет треугольника.
 |
Решение:
1. AC = 2r = 10 м
2. Пусть AM = AK = x, MC = CL = y
По теореме Пифагора:
![]() x + y = 10
x + y = 10
(x + 2)2 + (y + 2)2 = (x + y)2
![]() y = 10 – x
y = 10 – x
(x + 2)2 + (10 – x + 2)2 = (x + 10 – x)2
(x + 2)2 + (12 – x)2 = 100
x2 + 4x + 4 +144 – 24x + x2 = 100
2x2 – 20x + 148 = 100
2x2 – 20x + 48 = 0
x2 – 10x + 24 = 0
x1 = 6, x2 = 4
y = 10 – x
![]()
![]() x = 6 x = 4
x = 6 x = 4
y = 4 y = 6
3. Так как нужно найти больший катет, то берем y = 6
BC = 2 + 6 = 8 м
Ответ: BС = 8 м
Задача 5: окружность, вписанная в равнобедренный треугольник, касается его боковых сторон в точках K и A. Точка K делит сторону этого треугольника на отрезки 15 и 10, считая от основания. Найдите длину отрезка KA.
 |
Дано: ∆ BCD – равнобедренный, K є BC, A є DC, BK = 15, KC = 10
Найти: KA
Решение:
1. CD = CB = BK + KC, CD = CB = 15 + 10 = 25