Реферат: Парная линейная регрессия, парная нелинейная регрессия, множественная регрессия, временные ряды

1. Моделирование и идентификация парной линейной регрессии

1.1. План работы :

- синтез модели Монте-Карло парной линейной регрессии (прямая задача).

- вычисление параметров парной линейной регрессии (обратная задача идентификации.

- оценка существенности параметров линейной регрессии и доверительные интервалы линии регрессии.

- оценка доверительных интервалов прогноза.

- идентификация модели реальных экономических наблюдений (в соответствии с заданным вариантом).

1.2. Модель Монте-Карло линейной регрессии

1.2.1. Уравнение парной линейной регрессии

Парное линейное регрессионное уравнение имеет вид

, где (1.1)

x - независимая переменная (признак-фактор),

y - зависимая переменная (результативный признак),

a , b - параметры модели.

Данное уравнение определяет зависимость признак-фактора y от результативного признака x .

В реальности на данную связь оказывает влияние множество других неконтролируемых факторов, в связи, с чем данная связь представляется как:

, где (1.2)

e - случайное отклонение наблюдаемой зависимой переменной, вызванное влиянием других факторов. Данная величина распределена по центрированному нормальному закону со средним квадратическим отклонением σе . Задачей идентификации регрессионной модели является по данным реальных наблюдений зависимой (y ) и независимой (x ) переменным при наличии случайных отклонений (e ) оценить параметры регрессионной модели a и b .

Именно уравнение (1.2) является основой статистического моделирования уравнения регрессии.

1.2.2. Последовательность выполнения работы по моделированию :

1.2.2.1. Открываем новую книгу. Cохраняем книгу в папке под именем ПЛР. Xls (Парная Линейная Регрессия). Озаглавим лист «Модель».

1.2.2.2. Формируем заголовки для исходных данных модели (Рисунок 1.1):

- коэффициенты модели a , b ;

- объем наблюдений n ;

- среднее квадратическое отклонение погрешности СКОе ;

- математическое ожидание независимой переменной М_х ;

-среднее квадратическое отклонение независимой переменной СКО_х .

- коэффициент корреляции r ;

- коэффициент детерминации D .

Вводим n =100 и значения а , b , CKO_e (σ_е ), M_x , CKO_x .

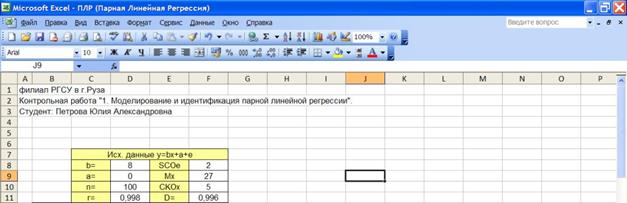
Рисунок 1. 1

1.2.2.3. Сформируем заголовки таблицы модели (Рисунок 1.2).