Реферат: Парная линейная регрессия, парная нелинейная регрессия, множественная регрессия, временные ряды
Колонки y=bx+a и e в расчете коэффициентов a и b участия не принимают, поскольку теоретическая зависимость и погрешность нам не известна. Именно их мы оцениваем по моделируемому фактическому значению y=bx+a+e .
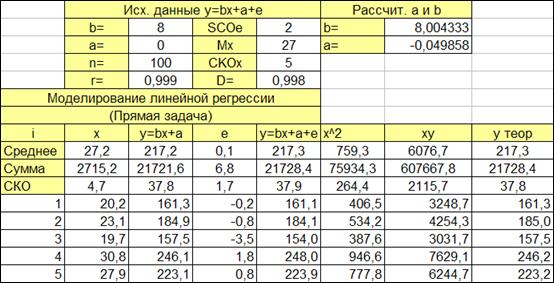
Рисунок 1.9
1.3.2.3. Рассчитаем значения xy , x2 .
1.3.2.4. Получим средние значения, входящие в формулы расчета коэффициентов a и b .
1.3.2.5. Рассчитаем коэффициенты a и b по формулам (1.15) и (1.16).
1.3.2.6. Сопоставим заданные коэффициенты a и b с рассчитанными.
1.3.2.7. Получим столбец идентифицированной (с рассчитанными коэффициентами линии регрессии a и b ) (Рисунок 1.9).
1.3.2.8. Добавим к графику факторной линии регрессии график идентифицируемой линии (с рассчитанными коэффициентами).
1.3.2.9. Увеличивая СКО случайного отклонения σе получаем два графика факторной и идентифицируемой линии регрессии (Рисунок 1.10).
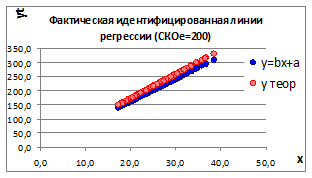
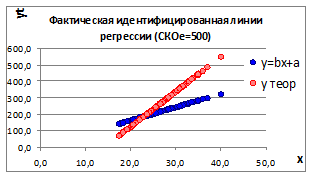
Рисунок 1.10
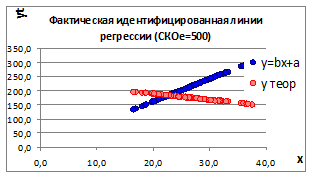

Рисунок 1. 11
1.3.2.10. При увеличении СКОе уменьшаются коэффициенты корреляции r и детерминации D , а, следовательно, уменьшается связь между изучаемыми параметрами. И это наглядно видно на графиках - несовпадение факторной и идентифицируемой линии регрессии.
1.3.2.11. Получим два наблюдения за процессом при одном и том же относительно большом СКОе и построим графики (Рисунок 1.11).
Изменение параметров линии регрессии происходит потому, что происходит изменение влияния случайных факторов на связь между изучаемыми параметрами.
1.4. Оценка существенности параметров линейной регрессии и корреляции.
1.4.1. Основные положения :
Общая сумма квадратов отклонения независимой переменой y может быть представлена суммой квадратов отклонения y и остаточной суммы квадратов переменной
![]() (1.17)
(1.17)
Scom Общая сумма квадратов отклонений | Sfact Сумма квадратов отклонений, обусловленная регрессией | Srem Остаточная сумма квадратов отклонений |
Средние квадраты данных отклонений вычисляется как:
![]() (1.18)
(1.18)
![]() (1.19)
(1.19)
![]() (1.20)
(1.20)
F -отношение определяется как:
 (1.21)
(1.21)
Нулевая гипотеза (об отсутствии связи между y и x ) принимается если:
![]() , где (1.22)
, где (1.22)
Ftable (1,n-2,α) - табличное значение F -критерия для степеней свободы 1 (числитель), n-2 (знаменатель),α - уровень значимости.
Гипотеза о наличии связи между y и x принимается если
![]() (1.23)
(1.23)
1.4.2. Порядок выполнения проверки нулевой гипотезы :
1.4.2.1. Сделаем копию листа и озаглавим его «Существенность параметров».
1.4.2.2. Сформируем заголовки таблицы модели (Рисунок 1.12).
1.4.2.3. Выделим ячейки для расчета:
- средних квадратов отклонений на одну степень свободы (Dcom , Dfact , Drem ),
- коэффициента детерминации D через суммы квадратов отклонений,
- средних квадратов отклонений,
- F -отношения, через средние квадратов отклонений на одну степень свободы,
- F -отношения, через коэффициент детерминации,
- табличного значения F -критерия,