Реферат: Парная линейная регрессия, парная нелинейная регрессия, множественная регрессия, временные ряды
Представим копию интерфейса с таблицей из первых 10-ти наблюдений и двух зависимостей (Рисунок 1.5).
1.2.2.13. Исследуем влияние параметров регрессионной модели на связь y(x) Исследуем влияние СКО ошибки регрессионной модели на коэффициент корреляции и детерминации. Изменяя СКО ошибки модели получаем моделируемые значения наблюдений (Рисунок 1.6, в верхней части приведены значения коэффициентов корреляции и детерминации).
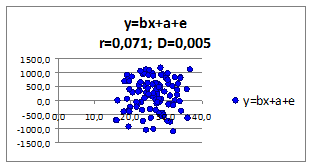
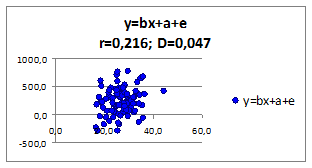
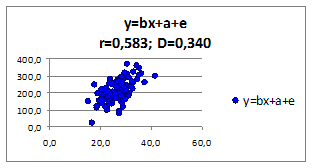
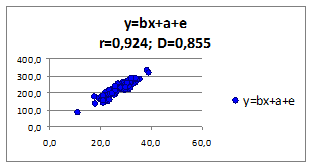
Рисунок 1. 6
Исследуем влияние коэффициента регрессии b на связь зависимой переменной от независимой. Построим графики для различных коэффициентов регрессии. Значения коэффициента регрессии b приведены в верхней части рисунка:
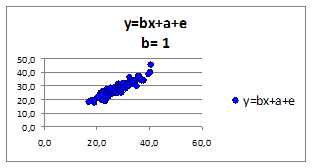
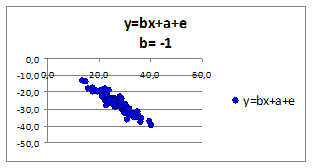
Рисунок 1.7
Исследуем влияние коэффициента а на связь зависимой переменной от независимой. Построим графики для различных коэффициентов а (а>0 , а<0 ). Значения коэффициента регрессии a приведены в верхней части рисунка:
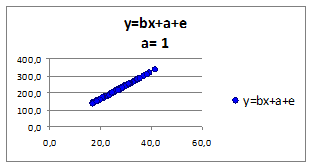
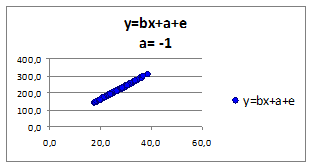
Рисунок 1.8
1.2.2.14. Сделаем выводы из полученных данных:
- знак коэффициента регрессии b имеет прямую связь со знаком коэффициента корреляции r . При изменении знака коэффициента регрессии b , меняется и знак коэффициента корреляции r .
- при уменьшении среднего квадратического отклонения σe , коэффициенты корреляции r и детерминации D увеличиваются.
- при изменении параметра a коэффициент эластичности не меняется.
- примеры регрессионных зависимостей в экономике с параметрами:
b>0 - зависимость средней заработной платы от среднедушевого прожиточного минимума в день одного трудоспособного человека.
b<0 - зависимость расходов на покупку продовольственных товаров (в общих расходах %) от среднедневной заработной платы одного работающего.
a>0 – зависимость расходов предприятия от объема производства.
a<0 -
1.3. Идентификация модели парной линейной регрессии
1.3.1. Основные положения процедуры идентификации :
Идентификация параметров модели основана на минимизации суммы квадратов отклонений наблюдаемой переменной от теоретической зависимости
![]() (1.7)
(1.7)
т.е. необходимо найти такие коэффициенты a и b , которые позволяют получить наименьшее значение суммы квадратов отклонений в данном выражении. Дифференцирование данного выражения по коэффициентам a и b , приравнивание производных нулю:
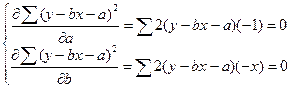 (1.8)
(1.8)
позволяет получить систему нормальных уравнений:
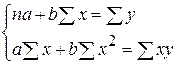 (1.9)
(1.9)
Поделив, левые и правые части на n получаем:
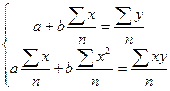 (1.10)
(1.10)
Данный метод вычисления коэффициентов называется методом наименьших квадратов (МНК). Выражая средние значения через оператор среднего:
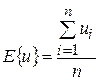 (1.11)
(1.11)
Система нормальных уравнений имеет вид:
![]() (1.12)
(1.12)
Решение данной системы уравнений относительно a и b на основе формулы Крамера имеет вид:
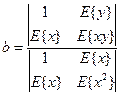 (1.13)
(1.13)
Коэффициент a может быть получен как:
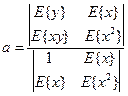 (1.14)
(1.14)
Данный коэффициент может быть получен также по формуле, вытекающей из теоретического уравнения линейной регрессии:
![]() , т.е. (1.15)
, т.е. (1.15)
![]() (1.16)
(1.16)
1.3.2. Последовательность выполнения :
1.3.2.1. Создаем копию листа «Модель» помещаем его перед листом «Лист2» и переименуем его назвав «Идентификация».
1.3.2.2. Выделяем ячейки (Рисунок 1.9) для расчета:
- коэффициентов a и b ,
- значений xy , x2 .