Реферат: Парная линейная регрессия, парная нелинейная регрессия, множественная регрессия, временные ряды

- номера наблюдения i ;

- независимой переменной x ;

- факторного значения зависимой переменной y , определяемой независимой переменной x ;

- ошибки регрессии (отклонение наблюдаемой независимой величины от фактического значения зависимой переменной y , определяемой независимой переменной x ) e ;

- наблюдаемого значения зависимой переменной (с учетом ошибки регрессии e ) y ;

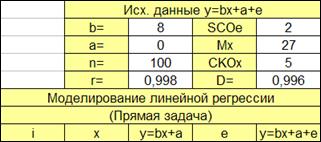
Рисунок 1.2

1.2.2.4. Сформируем заголовки строк для расчета (Рисунок 1.3) среднего, суммы, СКО соответствующих столбцов.

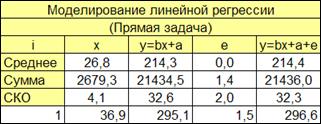
Рисунок 1.3

1.2.2.5. Вводим первый номер наблюдения (i=1 ) (Рисунок 1.3).

1.2.2.6. Смоделируем первое значение независимой переменной.

Случайное значение независимой переменной x моделируется нормальным законом распределения с заданными математическим ожиданием и средним квадратическим отклонением по формуле:

, где (1.3)

Z - центрированная и нормированная случайная величина, распределенная по нормальному закону (MZ=0 , σZ=1 ),

M_x , σ_x - математическое ожидание и среднее квадратическое отклонение независимой переменной.

Центрированная и нормированная случайная величина моделируется на основании центральной предельной теоремы путем 12-ти кратного сложения равномерно распределенных случайных чисел R_i в диапазоне (0,1].

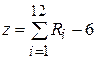(1.4)

Синтаксис функцией, возвращаемой случайное число, равномерно распределенное в диапазоне (0,1], имеет вид: R= слчис().

Таким образом, для моделирования независимой переменной необходимо в ячейку, где моделируется переменная x необходимо ввести формулу:

«=((слчис()+слчис()+слчис()+слчис()+слчис()+слчис()+слчис()+слчис()+слчис()+слчис()+слчис()+слчис()-6))*[ σ_x ] + [M_x ] », где

[M_x ] и [σ_x ] - соответственно адреса ячеек, где заданы математическое ожидание и среднее квадратическое отклонение независимой переменной.

Поскольку при копировании данные адреса, где заданы математическое ожидание и среднее квадратическое отклонение не должны изменяться, ссылки на них должны быть абсолютными.

1.2.2.7. Рассчитаем теоретическое значение зависимой переменной. Теоретическое значение зависимой переменной определяется формулой:

, (1.5)

1.2.2.8. Смоделируем ошибку модели.

Ошибка модели моделируется центрированным нормальным законом распределения аналогично моделированию независимой переменной по формуле: «=(слчис()+слчис()+слчис()+слчис()+слчис()+слчис()+слчис()+слчис()+слчис()+слчис()+слчис()+слчис()-6)*[ σ_e ] », где

[σ_e ] - абсолютная ссылка на ячейку, где задано среднее квадратическое отклонение ошибки регрессионной модели.

1.2.2.9. Рассчитаем фактическое значение зависимой переменной. Фактическое значение зависимой переменной рассчитывается как сумма теоретического значения и ошибки.

1.2.2.10. Моделируем сто наблюдений.

Пользуясь средствами копирования содержимого ячеек в Excel получаем 100 наблюдений независимой и зависимой переменной. В ячейку количества наблюдений n ввести 100.

1.2.2.11. Рассчитаем коэффициенты корреляции и детерминации.

В ячейку для коэффициента корреляции вводим функцию «коррел» из категории «статистические» для массивов зависимой и наблюдаемой независимой (с учетом ошибки) переменных.

Коэффициент детерминации равен:

, (1.6)

1.2.2.12. Рассчитаем средние, суммы и СКО :

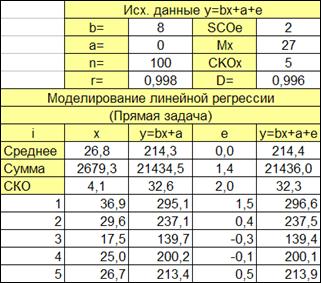
Рисунок 1. 4

В соответствующие ячейки независимой переменной вводим формулы расчета среднего значения, суммы и среднего квадратического отклонения.