Реферат: Применение дифференциального и интегрального исчисления к решению физических и геометрических задач в MATLab
В XVII в. были сделаны многие открытия, относящиеся к интегральному исчислению. Так, П. Ферма уже в 1629 г. решил задачу квадратуры любой кривой 
, где п — целое (т. е. по существу вывел формулу 
, и на этой основе решил ряд задач на нахождение центров тяжести.
Однако при всей значимости результатов, полученных многими чрезвычайно изобретательными математиками XVII столетия, исчисления еще не было. Необходимо было выделить общие идеи, лежащие в основе решения многих частных задач, а также установить связь операций дифференцирования и интегрирования, дающую достаточно общий алгоритм. Это сделали Ньютон и Лейбниц, открывшие независимо друг от друга факт, известный вам под названием формулы Ньютона — Лейбница. Тем самым окончательно оформился общий метод. Предстояло еще научиться находить первообразные многих функций, дать логические основы нового исчисления и т. п. Но главное уже было сделано: дифференциальное и интегральное исчисление создано.
Символ ∫ введен Лейбницем (1675 г.). Этот знак является изменением латинской буквы S (первой буквы слова summa ). Само слово интеграл придумал Я. Бернулли (1690 г.). Вероятно, оно происходит от латинского integro , которое переводится, как приводить в прежнее состояние, восстанавливать. (Действительно, операция интегрирования «восстанавливает» функцию, дифференцированием которой получена подынтегральная функция.) Возможно, происхождение термина интеграл иное: слово integer означает целый.
В ходе переписки И. Бернулли и Г. Лейбниц согласились с предложением Я. Бернулли. Тогда же, в 1696 г., появилось и название новой ветви математики — интегральное исчисление (calculus integralis ), которое ввел И. Бернулли.
Другие известные вам термины, относящиеся к интегральному исчислению, появились заметно позднее. Употребляющееся сейчас название первообразная функция заменило более раннее «примитивная функция», которое ввел Лагранж (1797 г.). Латинское слово primitivus переводится как «начальный»: 
— начальная (или первоначальная, или первообразная) для f(x), которая получается из F(х) дифференцированием.
В современной литературе множество всех первообразных для функции f(х) называется также неопределенным интегралом. Это понятие выделил Лейбниц, который заметил, что все первообразные функции отличаются на произвольную постоянную. А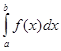 
называют определенным интегралом (обозначение ввел К. Фурье (1768—1830), но пределы интегрирования указывал уже Эйлер).
Методы математического анализа активно развивались в следующем столетии. В развитии интегрального исчисления приняли участие русские математики М. В. Остроградский (1801—1862), В. Я. Буняковский (1804-1889), П. Л. Чебышев (1821—1894).
Строгое изложение теории интеграла появилось только в прошлом веке. Решение этой задачи связано с именами О. Коши, одного из крупнейших математиков немецкого ученого Б. Римана (1826—1866, см. рис. 4.), французского математика Г. Дарбу (1842— 1917).
2. Дифференциал в физике
Мы ввели понятие дифференциала с помощью равенства 
. Для вычисления дифференциала надо найти производную. Однако, помня о том, что дифференциал — это главная часть приращения функции, линейно зависящая от приращений аргумента, мы из физических соображений получим равенства вида dy = kdx и сделаем вывод о том, что k — это производная у по х.
1. Работа. Найдем работу, которую совершает заданная сила F при перемещении по отрезку оси х. Если сила F постоянна, то работа А равна произведению F на длину пути. Если сила меняется, то ее можно рассматривать как функцию от х: F =F ( x ). Приращение работы А на отрезке [х, x + dx ] нельзя точно вычислить как произведение F ( x ) dx , так как сила меняется, на этом отрезке. Однако при маленьких dx можно считать, что сила меняется незначительно и произведение представляет главную часть 
, т. е. является дифференциалом работы (dA = = F ( x ) dx ). Таким образом, силу можно считать призводной работы по перемещению.
2. Заряд. Пусть q — заряд, переносимый электрическим током через поперечное сечение проводника за время t . Если сила тока / постоянна, то за время dt ток перенесет заряд, равный Idt . При силе тока, изменяющейся со временем по закону / = /(/), произведение I ( t ) dt дает главную часть приращения заряда на маленьком отрезке времени [/, t +- dt ], т.е.- является дифференциалом заряда: dq = I { t ) dt . Следовательно, сила тока является производной заряда по времени.
3. Масса тонкого стержня. Пусть имеется неоднородный тонкий стержень. Если ввести координаты так, как показано на рис. 130, то функция т= т(1) — масса куска стержня от точки О до точки /. Неоднородность стержня означает, что его линейная плотность не является постоянной, а зависит от положения точки / по некоторому закону р = р(/). Если на маленьком отрезке стержня [/, / + d/] предположить, что плотность постоянна и равна р(/), то произведение p(/)d/ дает дифференциал массы dm . Значит, линейная плотность — это производная массы по длине.
4. Теплота. Рассмотрим процесс нагревания какого-нибудь вещества и вычислим количество теплоты Q { T ), которое необходимо, чтобы нагреть 1 кг вещества от 0 °С до Т. Зависимость Q = Q ( T ) очень сложна и определяется экспериментально. Если бы теплоемкость с данного вещества не зависела от температуры, то произведение cdT дало бы изменение количества теплоты. Считая на малом отрезке [T , T + dT ] теплоемкость постоянной, получаем дифференциал количества теплоты dQ = c ( T ) dT . Поэтому теплоемкость — это производная теплоты по температуре.
5. Снова работа. Рассмотрим работу как функцию времени. Нам известна характеристика работы, определяющая ее скорость по времени, — это мощность. При работе с постоянной мощностью N работа за время dt равна Ndt . Это выражение представляет дифференциал работы, т.е. dA = N ( t ) dt , и мощность выступает как производная работы по времени.
Все приведенные примеры были построены по одному и тому знакомыми нам из курса физики: работа, перемещение, сила; заряд, время, сила тока; масса, длина, линейная плотность; и т. д. Каждый раз одна из этих величин выступала каккоэффициент пропорциональности между дифференциалами двумя других, т. е. каждый раз появлялось соотношение вида dy = k ( x ) dx . На такое соотношение можно смотреть как на способопределения величины k ( x ). Тогда k ( x ) находится (или определяется) как производная у по х. Этот вывод мы и фиксировали в каждом примере. Возможна и обратная постановка вопроса: как найти зависимость у от х из заданного соотношения междуих дифференциалами.
3. Приложения определенного интеграла к решению некоторых задач механики и физики
1. Моменты и центры масс плоских кривых. Если дуга кривой задана уравнением y = f ( x ), a ≤ x ≤ b , и имеет плотность 
= ( x ) , то статические моменты этой дуги Mx и My относительно координатных осей Ox и O y равны
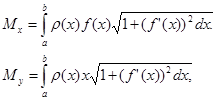
моменты инерции I Х и I у относительно тех же осей Ох и Оу вычисляются по формулам
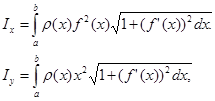
а координаты центра масс 
и 
— по формулам
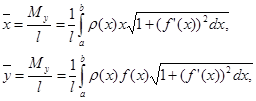
где l — масса дуги, т. е.
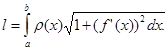
Пример 1. Найти статические моменты и моменты инерции относительно осей Ох
и Оу дуги цепной линии y = chx при 0≤ x ≤ 1.
◄ Имеем: 
Следовательно,
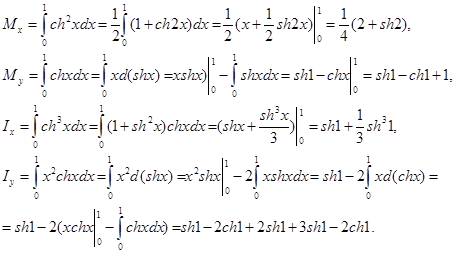
В приложениях часто оказывается полезной следующая
Теорема Гульдена . Площадь поверхности, образованной вращением дуги плоской кривой вокруг оси, лежащей в плоскости дуги и ее не пересекающей, равна произведению длины дуги на длину окружности, описываемой ее центром масс.