Реферат: Применение дифференциального и интегрального исчисления к решению физических и геометрических задач в MATLab

◄Вследствие симметрии . При вращении полуокружности вокруг оси Ох получается сфера, площадь поверхности которой равна , а длина полуокружности равна па. По теореме Гульдена имеем

Отсюда , т.е. центр масс C имеет координаты C .

2. Физические задачи. Некоторые применения определенного интеграла при решении физических задач иллюстрируются ниже в примерах.

Пример 4. Скорость прямолинейного движения тела выражается формулой (м/с). Найти путь, пройденный телом за 5 секунд от начала движения.

◄ Так как путь, пройденный телом со скоростью (t ) за отрезок времени [t₁ ,t₂ ], выражается интегралом

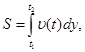
то имеем:

►

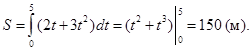4. Дифференциальные уравнения

Многие физические законы имеют вид дифференциальных уравнений, т. е. соотношений между функциями и их производными. Задача интегрирования этих уравнений — важнейшая задача математики. Одни дифференциальные уравнения удается проинтегрировать в явном виде, т.е. записать искомую функцию в виде формул. Для решения других до сих пор не удается найти достаточно удобных формул. В этих случаях можно найти приближенные решения с помощью вычислительных машин. Мы не будем подробно изучать методы интегрирования дифференциальных уравнений, а только рассмотрим несколько примеров.

Примеры

1. Уравнение механического движения. Пусть материальная точка массы т движется под действием силы F по оси х. Обозначим t время ее движения, и — скорость, а — ускорение. Второй закон Ньютона, а = Fm примет вид дифференциального уравнения, если записать ускорение, а как вторую производную: a = x ’’.

Уравнение тх" = F называют уравнением, механического движения, где x = x ( t ) —неизвестная функция, т и F — известные величины. В зависимости от условий задачи по-разному и записываются различные дифференциальные уравнения.

2. Радиоактивный распад

— масса распадающего вещества. Количество распадающего вещества пропорционально количеству и времени, т.е. при имеем

.

Решение дифференциального уравнения- . Дополнительные условия- , тогда задача

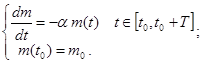
Решение задачи:

3.Движение системы N материальных точек.

Система уравнений Ньютона

,

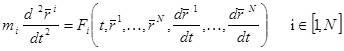-масса, - радиус вектор i- ой точки, - сила воздействующая на i -ую точку.

Частный случай колебания маятника

.

При малых колебаниях и тогда уравнение имеет вид:

.

4. Прогибание упругого стержня.

Если стержень однороден, то вдоль стержня постоянное касательное натяжение . Тогда вертикальная сила в точке x , где смещение u(x ). Если в каждой точке стержня действует внешняя сила то

.