Реферат: Принятие решений в условиях неопределенности
D3 = 25 r3 = 5
D4 = 10091/144 70.08 r4 8.37
Нанесем средние ожидаемые доходы и риски на плоскость — доход ![]() откладываем по вертикали, а риски — по горизонтали.
откладываем по вертикали, а риски — по горизонтали.
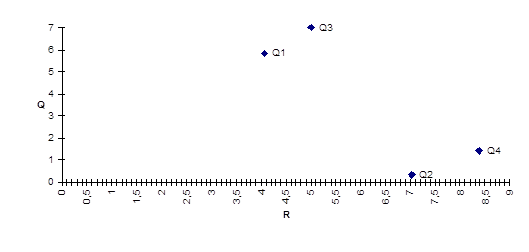
Получили четыре точки. Чем выше точка (q, r), тем более доходная операция, чем точка правее — тем более она рисковая. Значит, нужно выбирать точку левее и выше. Точка (q’, r’) доминирует точку (q, r), если q’q и r’r. В данном примере точка Q3 доминирует точки Q2 и Q4 , точка Q1 доминирует точки Q2 и Q4 . Точки Q1 и Q3 несравнимы — доходность 3-ей больше, но и риск ее тоже больше. Точка, не доминируемая никакой другой, называется оптимальной по Парето , а множество всех таких точек называется множеством оптимальности по Парето . Легко видеть, что если из рассмотренных операций надо выбрать лучшую, то ее обязательно надо выбирать из операций, оптимальный по Парето.
Предположим, что все операции независимы друг от друга, тогда можно выяснить, нет операции, являющейся линейной комбинацией основных операций, более хорошей, чем имеющиеся.
![]()
![]()
![]()
![]()
Теперь найдем ![]() , при которой риск будет минимальным. Т.к.
, при которой риск будет минимальным. Т.к. ![]() стремится к минимуму, то
стремится к минимуму, то ![]() также стремиться к минимуму.
также стремиться к минимуму.
![]()
![]()
График данной функции представляет собой параболу, ветви направлены вверх, значит, минимальное значение данной функции будет в точке перегиба — операция, являющаяся линейной комбинацией основных операций, будет иметь минимальный риск при ![]() . Этот риск будет равен 3.38, а доход соответственно 6,08.Полученная точка Q’(6.08, 3.38) доминирует точку Q1 (5.83,4.07).
. Этот риск будет равен 3.38, а доход соответственно 6,08.Полученная точка Q’(6.08, 3.38) доминирует точку Q1 (5.83,4.07).
Для нахождения лучших операций иногда применяют подходящую взвешивающую формулу, которая для пар (q, r) дает одно число, по которому и определяют лучшую операцию.
Для анализа ситуаций применим взвешивающую формулу E(Q, r) = 4Q - r. Данная формула говорит, что доход ценится в четыре раза больше, чем риск, т.е. увеличение риска на 4 компенсируется увеличением дохода на единицу.
Тогда для 1-ой операции Е = 19.25, для 3-ей операции Е = 23. При сравнении результатов анализа видно, что при данном отношении к рискованности операций лучшей является 3-я операция.
Часть III . Анализ денежных потоков.
Анализ одномерных денежных потоков.
Исходные данные: ежедневные суммарные зачисления по счетам юридических лиц за апрель месяц.
| число месяца | день недели | сумма (тыс. руб) | ||||
| 1 | ср | 47 | ||||
| 2 | чт | 44 | ||||
| 3 | пт | 31 | ||||
| 4 | сб | 28 | ||||
| 5 | вс | |||||
| 6 | пн | 42 | ||||
| 7 | вт | 48 | ||||
| 8 | ср | 39 | ||||
| 9 | чт | 40 | ||||
| 10 | пт | 38 | ||||
| 11 | сб | 15 | ||||
| 12 | вс | |||||
| 13 | пн | 45 | ||||
| 14 | вт | 53 | ||||
| 15 | ср | 41 | ||||
| 16 | чт | 27 | ||||
| 17 | пт | 56 | ||||
| 18 | сб | 25 | ||||
| 19 | вс | |||||
| 20 | пн | 51 | ||||
| 21 | вт | 32 | ||||
| 22 | ср | 49 | ||||
| 23 | чт | 21 | ||||
| 24 | пт | 35 | ||||
| 25 | сб | 13 | ||||
| 26 | вс | |||||
| 27 | пн | 58 | ||||
| 28 | вт | 59 | ||||
| 29 | ср | 29 | ||||
| 30 | чт | 30 | ||||
| числовой ряд (хi ) | частота (mi ) | частость ( | выборочная функция распределения | |||
| 13 | 1 | 0,04 | 0,04 | |||
| 15 | 1 | 0,04 | 0,08 | |||
| 21 | 1 | 0,04 | 0,12 | |||
| 25 | 1 | 0,04 | 0,15 | |||
| 27 | 1 | 0,04 | 0,19 | |||
| 28 | 1 | 0,04 | 0,23 | |||
| 29 | 1 | 0,04 | 0,27 | |||
| 30 | 1 | 0,04 | 0,31 | |||
| 31 | 1 | 0,04 | 0,35 | |||
| 32 | 1 | 0,04 | 0,38 | |||
| 35 | 1 | 0,04 | 0,42 | |||
| 38 | 1 | 0,04 | 0,46 | |||
| 39 | 1 | 0,04 | 0,50 | |||
| 40 | 1 | 0,04 | 0,54 | |||
| 41 | 1 | 0,04 | 0,58 | |||
| 42 | 1 | 0,04 | 0,62 | |||
| 44 | 1 | 0,04 | 0,65 | |||
| 45 | 1 | 0,04 | 0,69 | |||
| 47 | 1 | 0,04 | 0,73 | |||
| 48 | 1 | 0,04 | 0,77 | |||
| 49 | 1 | 0,04 | 0,81 | |||
| 51 | 1 | 0,04 | 0,85 | |||
| 53 | 1 | 0,04 | 0,88 | |||
| 56 | 1 | 0,04 | 0,92 | |||
| 58 | 1 | 0,04 | 0,96 | |||
| 59 | 1 | 0,04 | 1,00 | |||
График выборочной функции распределения ![]() .
.
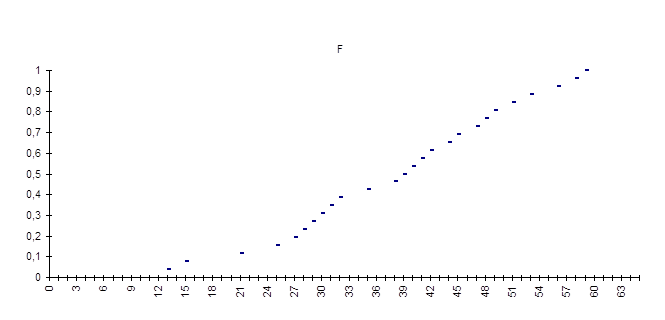
Теперь построим интервальный вариационный ряд. Рассчитаем длину интервала по формуле ![]() , где а — верхняя граница и b — нижняя граница для интервалов, v — количество интервалов. Для данного примера а = 59, b = 13, v = 6, а h = 9.
, где а — верхняя граница и b — нижняя граница для интервалов, v — количество интервалов. Для данного примера а = 59, b = 13, v = 6, а h = 9.
интер-валы [ai -ai+1 ) | сере- дина интер-вала (yi ) | частота (mi ) | частость ( | выборочная функция распределе-ния
| выборочная плотность ( |
| 9-18 | 13,5 | 2 | 0,08 | 0,08 | 0,22 |
| 18-27 | 22,5 | 2 | 0,08 | 0,16 | 0,22 |
| 27-36 | 31,5 | 7 | 0,27 | 0,43 | 0,78 |
| 36-45 | 40,5 | 6 | 0,23 | 0,66 | 0,67 |
| 45-54 | 49,5 | 5 | 0,19 | 0,85 | 0,56 |
| 54-63 | 58,5 | 4 | 0,15 | 1 | 0,44 |
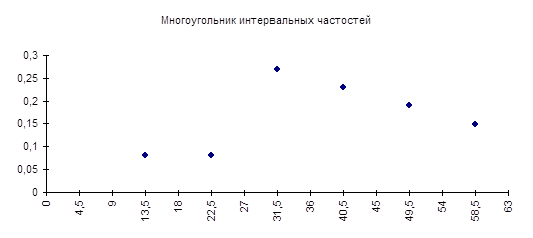
График функции распределения ![]() выглядит следующим образом.
выглядит следующим образом.
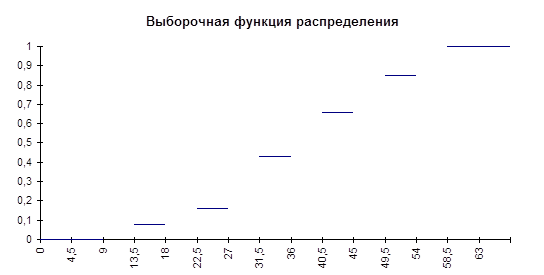
Многоугольник интервальных частостей дает более наглядное представление о закономерности изменения ежедневных денежных потоков, т.к. суммы зачислений в разные дни различны и их можно анализировать только по их вхождению в какой-либо интервал.
Выборочное среднее считается следующим способом:
1. непосредственно по исходным данным 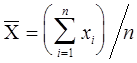 ,
, ![]() .
.
2. по дискретному вариационному ряду
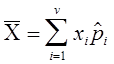 , где v — число вариантов выборки, но в данном примере v = n .
, где v — число вариантов выборки, но в данном примере v = n . ![]() .
.