Реферат: Принятие решений в условиях неопределенности

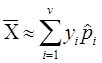, таким образом можно найти лишь приближенное значение выборочной средней. .

Аналогом дисперсии является выборочная дисперсия:

1. непосредственно по исходным данным , .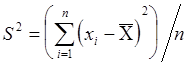

2. по дискретному вариационному ряду ,.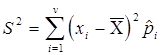

3. по интервальному вариационному ряду приблизительное значение , .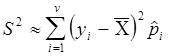

Среднее квадратическое отклонение рассчитывается как квадратный корень из дисперсии.

1.

2.

3.

Исследуемая нами большая совокупность называется генеральной совокупностью . Теоретически может быть бесконечной В данном примере выборка состоит из 26 элементов. Понятия генеральной совокупности и случайной величины взаимозаменяемы.

Любая функция от выборки называется статистикой .

Пусть — некоторый параметр с.в. Х. Мы хотим определить хотя бы приближенно, значение этого параметра. С этой целью подбираем статистику , которая должна оценивать, может быть приближенно, параметр .

Заметим, что любая статистика есть с.в., поскольку она определена на выборках. Статистику , определенную на выборках объемом n , будем обозначать.

Статистика должна удовлетворять следующим требованиям:

1. состоятельность. Статистика-оценка должна сходиться к оцениваемому параметру при .

2. несмещенность. для всех достаточно больших n .

Генеральная средняя удовлетворяет обоим условиям, поэтому составляет , но генеральная дисперсия удовлетворяет лишь первому условия, поэтому ее “подправляют”, умножая на