Реферат: Различные подходы к определению проективной плоскости

Теорема 1: Через две различные () проходит единственная прямая.

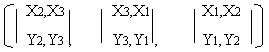Доказательство: 1) Существование. Пусть Х= {(Х1,Х2,Х3)} и У={(Y1,Y2,Y3)} две различные (). Определим прямую следующим образом:

C= Х*Y то есть С =

так как CХ = (Х*Y)Х = |Х,Y,Х| = 0

CY = (Х*Y)Y = |Х,Y,Y| = 0

и по свойству определителей, то () Х и Y принадлежат прямой С.

2) Единственность. Если прямая С={(C1,C2,C3)} содержит () Х и Y, то любой представитель (C1,C2,C3) класса С удовлетворяет системе уравнений.

C1Х1 + C2Х2 + C3Х3 =0

C1Y1 + C2Y2 + C3Y3 =0 (5)

$ бесконечное множество ненулевых решений этой системы (нулевое решение не определяет прямую). При этом для " решения (С1,С2,С3) справедливо равенство:

{(C1,C2,C3 )}= Х2,Х3 Х3,Х1 Х1,Х2

Y2,Y3 , Y3,Y1 , Y1,Y2

Т.е. решения системы (5) образуют единственный класс ненулевых троек. Этот класс определяет единственную прямую С. ч.т.д.

Теорема 2: Две различные прямые имеют единственную общую точку.

Доказательство: Пусть, С={(С1,С2,С3)}, m={(m 1,m 2,m 3)} две различные прямые. Найдем () Х ={(Х1,Х2,Х3)}, лежащую на этих прямых. Достаточно повторить доказательство предыдущей теоремы, заменив Х на С, Y на m , С на Х. Получим, что единственная общая точка Х определяется равенством

Х=С*m (6). ч.т.д.

Теорема 3: Для того, чтобы три () Х,Y,Z лежали на одной прямой, необходимо и достаточно, чтобы

Х1 Х2 Х3

|X,Y,Z|=0 (7), то есть Y1 Y2 Y3 =0

Z1 Z2 Z3

Доказательство: 1)Необходимость. Пусть () X,Y,Z лежат на одной прямой С. если хотя бы две из них совпадают, то равенство (7) следует из определения смешенного произведения и свойств определителя. Пусть эти () различны. Пользуясь теоремой 1, можно записать C=X*Y. Так как ()Z лежит на прямой C, то CZ=0 Þ (X*Y)Z=|X,Y,Z|=0

2)Достаточность. Пусть выполняется равенство (7). Рассмотрим произведение C=X*Y. Равенство (7) можно записать в виде (X*Y)Z=0, то есть CZ=0 Þ()z лежит на прямой C проходящей через () X и Y. Равенство (7) не зависит от выбора представителей точек.

Теорема доказана.

Теорема 4: Для того, чтобы три прямые c, m, n проходили через одну () необходимо и достаточно, чтобы

|c,m,n|=0 (8)

Для троек действительных чисел понятие линейной зависимости и линейной независимости определяется так же, как и для векторов. Пусть тройки x,…, x линейно зависимы. Легко проверить, что " другие тройки x,…, x, принадлежащие тем же классам, тоже линейно зависимы. Поэтому классы троек (точки) линейно зависимы, если линейно зависимы какие-нибудь представители этих классов.

Из теорем 3 и 4 следуют две теоремы.

Теорема 5: Для того, чтобы три () лежали на одной прямой, необходимо и достаточно, чтобы они были линейно зависимы.

Теорема 6: Для того, чтобы три прямые проходили через одну (), необходимо и достаточно, чтобы они были линейно зависимы.

2.3. Теорема Дезарга.

На проективной действительной плоскости имеет место теорема Дезарга.