Реферат: Разностные аппроксимации

a₁ = k_1/2 + O(h² )

получим

Отсюда имеем

Учитывая граничное условие (2), получаем

l_h u(0) = 0,5h [– (ku’)’(0) + d₀ u₀ – j ₀ ] + O(h² ) .

Выражение, стоящее в квадратных скобках, преобразуем, учитывая уравнение (1), к виду

– (ku’)’(0) + d₀ u₀ – j ₀ = – (ku’)’(0) + q(0)u(0) – f(0) +

+ (d₀ – q(0))u₀ – (f(0) – j ₀ ) = (d₀ – q(0))u₀ – (f(0) – j ₀ ) .

Из соотношений

получаем

что и требовалось доказать.

Таким образом, при достаточной гладкости коэффициентов k(x), q(x), f(x) и решения u(x) разностная схема (10) аппроксимирует исходную задачу (2) со вторым порядком по h .

При практическом использовании разностной схемы для нахождения ее коэффициентов не обязательно вычислять интегралы (4), (6) точно. Можно воспользоваться коэффициентами, полученными путем замены этих интегралов квадратурными формулами, имеющими точность O(h² ) и выше. Например, в результате применения формулы прямоугольников получим следующие коэффициенты: a_i = k(x_i – 0,5h), d_i = q(x_i ), j _i = f(x_i ).

Применяя формулу трапеций, получим

Представление коэффициентов разностной схемы в виде интегралов (4), (6) оказывается полезным при исследовании сходимости в случае разрывных функций k(x), q(x), f(x) .

2.3. Уравнение для погрешности. Решение y_i = y(x_i ) разностной задачи (3), (4) зависит от шага h сетки, y(x_i ) = y_h (x_i ) . По существу, мы имеем семейство решений {y_h (x_i )} , зависящее от параметра h . Говорят, что решение y_h (x) разностной задачи сходится к решению u(x) исходной дифференциальной задачи, если при h®0 погрешность y_h (x_i ) – u(x_i ), i = 0, 1,…, N , стремится к нулю в некоторой норме. В настоящем параграфе в качестве такой нормы будем брать норму в сеточном пространстве C( w _h ) , т.е. положим

Говорят, что разностная схема имеет m-й порядок точности (или сходится с порядком m ), если

где m>0, M>0 – константы, не зависящие от h .

Выше было установлено, что схема (3), (4) имеет второй порядок аппроксимации. Докажем теперь, что эта схема имеет и второй порядок точности. Для этого прежде всего выпишем уравнение, которому удовлетворяет погрешность z_i = y_i – u(x_i ) . Поставим y_i = z_i + u(x_i ) в уравнения (3), (4). Тогда получим уравнения

(11)

(12)

где обозначено

Функция y _i , входящая в правую часть уравнения (11), называется погрешностью аппроксимации дифференциального уравнения (1) разностным уравнением (3) на решении задачи (1), (2). В п.1 было доказано, что y _i = O(h² ) при h®0, i=1, 2,…, N–1 . Аналогично, величина n₁ является по определению погрешностью аппроксимации краевого условия (2) разностным краевым условием (4) на решении задачи (1), (2), причем n ₁ =O(h² ) . Таким образом, структура уравнений для погрешности (11), (12) та же, что и у разностной схемы (3), (4), отличаются только правые части.

Чтобы доказать сходимость разностной схемы, оценим решение задачи (11), (12) через правые части y _i , n ₁ , т.е. получим неравенство вида

(13)

с константой M₁ , не зависящей от h . Из этого неравенства и будет следовать, что

Отметим, что неравенства вида (13), называемые априорными оценками, нашли широкое применение в теории разностных схем. Поскольку структура для погрешности (11), (12) та же, что и у разностной схемы (3), (4), а отличаются только правые части, то оценка (13) выполняется одновременно с аналогичной оценкой

для разностной схемы (3), (4) при m ₂ = 0 . Последняя оценка выражает устойчивость решения разностной задачи по правым частям j и m ₁ .

2.4. Разностные тождества и неравенства. Для того, чтобы доказать неравенство (13), нам потребуются некоторые разностные тождества и неравенства. Будем рассматривать сеточные функции, заданные на сетке (7). Обозначим
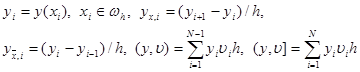