Реферат: Разностные аппроксимации

(y, u _x ) = –( u , y_x ) + y_N u _N – y₀ u ₁ . (14)

Действительно,

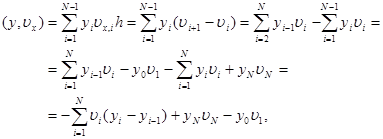что и требовалось доказать. Тождество (14) называется формулой суммирования по частям .

Подставляя в (14) вместо u выражение az_x и вместо y функцию z, получаем первую разностную формулу Грина

(15)

Здесь В частности, если z_N = 0 (как в задаче (11), (12)), то получим

(16)

Обозначим

и докажем, что для любой сеточной функции z_i , удовлетворяющей условию z_N = 0 , справедливо неравенство

(17)

Для доказательства воспользуемся тождеством

и применим неравенство Коши-Буняковского

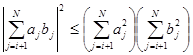Тогда получим

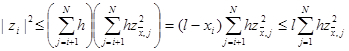Откуда сразу следует неравенство (17).

2.5. Доказательство сходимости. Возвращаясь к доказательству сходимости схемы (3), (4), получим тождество, которому удовлетворяет погрешность z_i = y_i – u(x_i ) . Для этого умножим уравнение (11) на hz_i и просуммируем по i от 1 до N–1 . Тогда получим

Отсюда, применяя разностную формулу Грина (16), получим

Далее, согласно (12) имеем

следовательно, справедливо тождество

(18)

Из этого тождества и будет сейчас выведено требуемое неравенство вида (13).

Заметим прежде всего, что если

k(x) ³ c₁ > 0, b ³ 0, q(x) ³ 0,

то коэффициенты разностной схемы (3), (4) удовлетворяют неравенствам

a_i ³ c₁ > 0, b ³ 0, d_i ³ 0. (19)

Это утверждение сразу следует из явного представления коэффициентов (5), (6).

Воспользовавшись (19), оценим слагаемые, входящие в левую часть тождества (18), следующим образом:

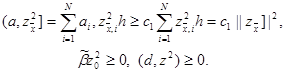Тогда придем к неравенству

(20)

Оценим сверху правую часть этого неравенства. Будем иметь
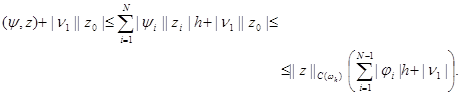