Реферат: Разностные аппроксимации

т.е.

Окончательно

(21)

Поскольку из неравенства следует,

что погрешность z_i = y_i – u(x_i ) также является величиной O(h² ) при h®0. Итак, справедливо следующее утверждение.

Пусть k(x) – непрерывно дифференцируемая и q(x), f(x) – непрерывные функции при x Î [0, l], решение u(x) задачи (1), (2) обладает непрерывными четвертыми производными. Пусть коэффициенты разностной схемы (3), (4) удовлетворяют условиям (8), (9), (19). Тогда решение разностной задачи (3), (4) сходится при h ® 0 к решению исходной дифференциальной задачи (1), (2) со вторым порядком по h, так что выполняется оценка

где M – постоянная, не зависящая от h.

3. Разностные схемы для уравнения теплопроводности

3.1. Исходная задача. Будем рассматривать следующую первую краевую задачу для уравнения теплопроводности с постоянными коэффициентами. В области {0 < x < 1, 0 < t £ T} требуется найти решение уравнения

(1)

удовлетворяющее начальному условию

u(x, 0) = u₀ (x) (2)

и граничным условиям

u(0, t) = m ₁ (t), u(1, t) = m ₂ (t). (3)

Здесь u0(x), m ₁ (t), m ₂ (t) – заданные функции. Известно, что при определенных предположениях гладкости решение задачи (1)–(3) существует и единственно. В дальнейшем при исследовании аппроксимации разностных схем будем предполагать, что решение u(x, t) обладает необходимым по ходу изложения числом производных по x и по t. Решение задачи (1) – (3) удовлетворяет принципу максимума и тем самым непрерывно зависит от начальных и граничных данных.

3.2. Явная схема. Как всегда, для построения разностной схемы надо прежде всего ввести сетку в области изменения независимых переменных и задать шаблон, т.е. множество точек сетки, участвующих в аппроксимации дифференциального выражения. Введем сетку по переменному x такую же, как в предыдущей главе, т.е.

w _h = {x_i = ih, i = 0, 1,…, N, hN = 1}

и сетку по переменному t с шагом t, которую обозначим

w _t = {t_n = n t , n = 0, 1,…, K, K t = T}

Точки (x_i , t_n ), i = 0, 1,…, N, n = 0, 1,…, K , образуют узлы пространственно-временной сетки w_{h, t} = w_h x w_t . Узлы (x_i , t_n ) , принадлежащие отрезкам I₀ = {0 £ x £ 1, t = 0}, I₁ = {x = 0, 0 £ t £ T}, I₂ = {x = 1, 0 £ t £ T} , называются граничными узлами сетки w_{h, t} , а остальные узлы – внутренними. На рисунке граничные узлы обозначены крестиками, а внутренние – кружочками.

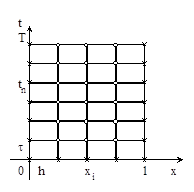Слоем называется множество всех узлов сетки w_{h, t} , имеющих одну и ту же временную координату. Так, n-м слоем называется множество узлов

(x₀ , t_n ), (x₁ , t_n ),…, (x_N , t_n ) .

Для функции y(x, t) , определенной на сетке w_{h, t} , введем обозначения yⁿ _i = y(x_i , t_n ) ,

(4)

Иногда для упрощения записи индексы i и n будем опускать, обозначая

( x_i , t_n+1 ) (x_i-1 , t_n+1 ) (x_i , t_n+1 ) (x_i+1 , t_n+1 )

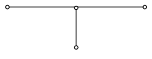(x_i-1 , t_n ) (x_i , t_n ) (x_i+1 , t_n ) (x_i , t_n )

(x_i-1 , t_n+1 ) (x_i , t_n+1 ) (x_i+1 , t_n+1 ) (x_i , t_n+1 )

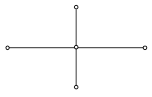(x_i-1 , t_n ) (x_i , t_n ) (x_i+1 , t_n ) (x_i-1 , t_n ) (x_i , t_n ) (x_i+1 , t_n )