Реферат: Разностные аппроксимации

следовательно, |q| £ 1 при любых j , t , h . Таким образом, схема (12) абсолютно устойчива, т.е. устойчива при любых шагах t и h . Абсолютная устойчивость является основным условием неявных схем. Теперь уже не надо брать шаг t слишком малым, можно взять, например, t = h = 10^-2 . Величина шагов сетки t , h определяются теперь необходимой точностью расчета, а не соображениями устойчивости.

Шеститочечной симметричной схемой называется разностная схема

(14)

для которой начальные и граничные условия задаются так же, как и в схеме (12). Эта схема использует шеститочечный шаблон, изображенный на рисунке.

Обобщением трех рассмотренных схем является однопараметрическое семейство схем с весами. Зададим произвольный действительный параметр s и определим разностную схему

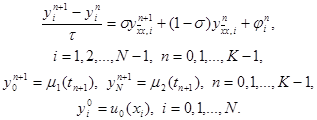(15)

При s = 0 получим отсюда явную схему, при s = 1 – чисто неявную схему и при s = 0,5 – симметричную схему (14). Исследуем погрешность аппроксимации схемы (15) на решении исходной задачи (1) – (3). Представим решение задачи (15) в виде y_i ⁿ = u(x_i , t_n ) + z_i ⁿ , где u(x_i , t_n ) – точное решение дифференциальной задачи (1) – (3). Тогда для погрешности получим систему уравнений

(16)

i = 1, 2,…, N – 1, n = 0, 1,…, K – 1,

z₀ ⁿ⁺¹ = z_N ⁿ⁺¹ = 0, n = 0, 1,…, K – 1, z_i ⁰ = 0, i = 0, 1,…, N.

Сеточная функция y_i ⁿ , входящая в правую часть уравнения (16) и равная

(17)

называется погрешностью аппроксимации схемы (15) на решении задачи (1) – (3). Получим первые члены разложения функции y_i ⁿ по степеням h и t. Будем разлагать все функции, входящие в выражение для y_i ⁿ , по формуле Тейлора в точке (x_i , t_n + 0,5t). Учитывая разложения

где

получим

Отсюда, проводя разложение в точке (x_i , t_n+1/2 ) и обозначая u = u (x_i , t_n+1/2 ) , будем иметь

и, перегруппировывая слагаемые, получим, что

Учитывая уравнение (1) u’’ – u = – f и следствие из него u^IV – u’’ = –f’’ , окончательно можно записать, что

(18)

Из формулы (18) можно сделать следующие выводы. Если

то схема (15) имеет второй порядок аппроксимации по t и четвертый – по h . Такая схема называется схемой повышенного порядка аппроксимации. Если

то схема (15) имеет второй порядок аппроксимации по t и по h. При остальных значениях s и при j _i ⁿ º 0 в виде (10), то получим

и |q| £ 1 при всех j, если

(19)

Отсюда видно, в частности, что все схемы с s³ 0,5 абсолютно устойчивы. Схема повышенного порядка аппроксимации (s = s_* ) также абсолютно устойчива, что проверяется непосредственно.

При s¹ 0 разностная схема (15) является неявной схемой. Для нахождения решения y_i ⁿ⁺¹ по заданным y_i ⁿ требуется решать систему уравнений

(20)

где

Система (20) решается методом прогонки. Условия устойчивости прогонки при s¹ 0 сводятся к неравенству

|1 + 2 s g | ³ 2 | s | g

и выполнены при s³ – 1/(4g). Последнее неравенство следует из условия устойчивости (19) разностной схемы.