Реферат: Решение дифференциального уравнения с последующей аппроксимацией

x₂ = 0.75 + 0.05 = 0.8

y_2* = 2.097665 + 0.05 * (- 0.022389) = 2.096546

y₂ = 2.097665 + 0.05 * ((- 0.022389) + 0.026314) / 2 = 2.097763

f( x₂ ; y₂ ) = 0.8 + cos (2.097763 / Ö0.3 ) = 0.027724

x₃ = 0.8 + 0.05 = 0.85

y_3* = 2.097763 + 0.05 * 0.027724 = 2.0991492

y₃ = 2.097763 + 0.05 * (0.027724 + 0.079334) / 2 = 2.10044

f( x₃ ; y₃ ) = 0.85 + cos (2.10044 / Ö0.3 ) = 0.080838

x₄ = 0.85 + 0.05 = 0.9

y_4* = 2.10044 + 0.05 * 0.080838 = 2.1044819

y₄ = 2.10044 + 0.05 * (0.080838 + 0.135575) / 2 = 2.10585

f( x₄ ; y₄ ) = 0.9 + cos (2.10585 / Ö0.3 ) = 0.137188

x₅ = 0.9 + 0.05 = 0.95

y_5* = 2.10585 + 0.05 * 0.137188 = 2.1127094

y₅ = 2.10585 + 0.05 * (0.137188 + 0.195345) / 2 = 2.114164

f( x₅ ; y₅ ) = 0.95 + cos (2.114164 / Ö0.3 ) = 0.19709

x₆ = 0.95 + 0.05 = 1

y_6* = 2.114164 + 0.05 * 0.19709 = 2.1240185

y₆ = 2.114164 + 0.05 * (0.19709 + 0.259053) / 2 = 2.125567

Для оценки погрешности вычислений используется правило Рунге:

y_i+1 = y_ih + (y_{ih /2} - y_ih ) / (2^p - 1) , где:

р - порядок метода, для Эйлера - Коши р = 2

Рассчитаем погрешность вычисления в точке х = 1. Найдем уточненное решение:

y₍₁₎ = 2.125049 + (2.125567 - 2.125049) / (2² - 1) = 2.1252216

e _ih = 2^p (y_ih - y_{ih /2} ) / (2^p - 1) = 2² (2.125567 - 2.125049) / 3 = 6.9 * 10 ^-4

e _{ih /2} = (y_ih - y_{ih /2} ) / (2^p - 1) = (2.125567 - 2.125049) / 3 = 1.73 * 10 ^-4

Таблица 1. Значения X и Y, полученные с помощью ручного расчёта.

I	X ( I )	Y ( I )
0	0.7	2.1
1	0.8	2.09763
2	0.9	2.105547
3	1	2.125049
4	1.1	2.157721
5	1.2	2.205613
6	1.3	2.271475
7	1.4	2.359045
8	1.5	2.473328
9	1.6	2.620626
10	1.7	2.807662

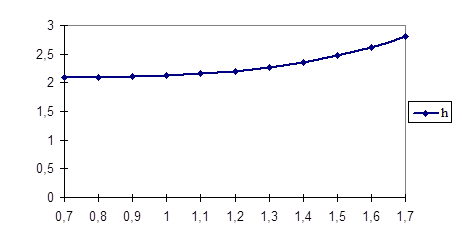
График решения дифференциального уравнения представлен на рисунке 3.

2. АППРОКСИМАЦИЯ. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ

2.1. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Исходя из постановки задачи, нужно аппроксимировать полученное в п.1. решение ( Таблица 1. ) параболой методом наименьших квадратов, т.е. нужно найти функцию, в данном случае параболу, которая в точках X ( I ) принимала бы значения, как можно более близкие к значениям Y ( I ). Парабола является функцией с тремя параметрами: F (x) = ax² + bx + c

Сумма квадратов разностей значений функции и решений дифференциального уравнения (Таблица 1.) должна быть минимальной, т.е.:

( ax² + bx + c - y_i )² => min

Функция будет иметь минимум, когда все частные производные равны нулю.

DF / da = 0, dF / db = 0, dF / dc = 0

После преобразований получим систему уравнений:

a₁₁ a + a₁₂ b + a₁₃ c = b₁

a₂₁ a + a₂₂ b + a₂₃ c = b₂

a₃₁ a + a₃₂ b + a₃₃ c = b₃

где a₁₁ = , a₁₂ = a₂₁ = , a₁₃ = a₂₂ = a₃₁ = , a₂₃ = a₃₂ =x_i , a₃₃ = n + 1