Реферат: Системи випадкових величин

(незалежність випадкових величин).

З використанням сумісного розподілу системи випадкових величин та моментів можна строго довести властивості математичного сподівання випадкової величини (3.3.1.5) та (3.3.1.6)

Доведення 3-ї властивості математичного сподівання . За означенням для дискретних величини

.

Для неперервних величин

Доведення 4-ї властивості математичного сподівання. За означенням для дискретних величини

.

(враховано, що для незалежних подій )

Для неперервних величин

.

Умовні початкові та центральні моменти порядку k компонент означаються рівностями

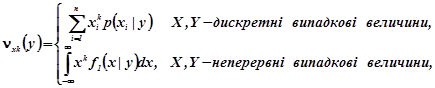(2.12a)

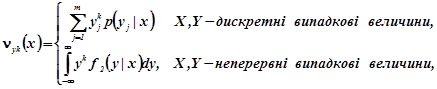(2.12b)

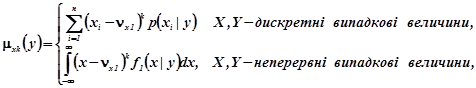(2.13а)

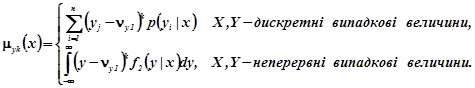(2.13b)

Найбільш важливими серед умовних моментів є умовні математичні сподівання компонент

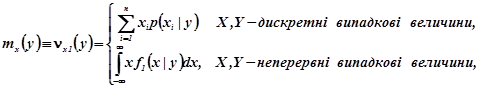(2.14а)

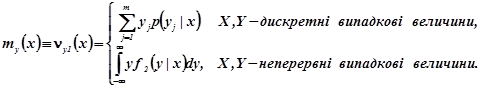(2.14b)

Умовні математичні сподівання компонент характеризують зв’язок між випадковими величинами Умовне математичне сподівання компоненти Y є функцією x і називається функцією регресії Y на X . Аналогічно, умовне математичне сподівання компоненти X є функцією y і називається функцією регресії X на Y .

Приклад 2.2.Дискретна випадкова величина задана сумісним розподілом

y₁ =3y₂ =6

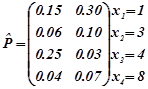
Необхідно обчислити функцію регресії Y на X та функцією регресії X на Y.

Розв’язування .За означенням (2.14b) регресія Y на X

. (1*)

За формулою (1.1a)