Реферат: Системи випадкових величин

при і

при .

У підсумку

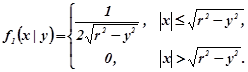
Аналогічно за формулою (1.11b)

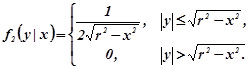
Як і будь-які інші густини розподілу, умовні ймовірності мають такі властивості

,

.

Дві випадкові величини є незалежними , якщо закон розподілу однієї з них не залежить від значення іншої. Умовні розподіли незалежних величин дорівнюють їх розподілам:

для неперервних величин і

.

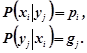для дискретних випадкових величин.

Необхідною та достатньою умовою незалежності випадкових величин є

,(1.12а)

або, як наслідок,

.(1.12b)

2. Характеристики системи двох випадкових величин

Система двох випадкових величин з достатньою точністю може характеризуватися початковими та центральними моментами компонент порядку , які є числами і тому називаються чисельними характеристиками, і умовними початковими та центральними моментами компонент порядку , які є функціями можливих значень компонент.

Початкові та центральні моменти означаються рівностями

(2.1а)

(2.1б)

Найбільш важливими серед них є математичне сподівання компонент, дисперсії компонент та кореляційний момент.

Математичні сподівання компонент означаються так:

(2.2а)

(2.2б)

З використанням математичних сподівань компонент початкові та центральні моменти системи двох випадкових величин можна означити більш зручним способом:

,(2.3а)